Dynamic Multisensory Integration: Somatosensory Speed Trumps Visual Accuracy during Feedback Control
- PMID: 27535908
- PMCID: PMC6601898
- DOI: 10.1523/JNEUROSCI.0184-16.2016
Dynamic Multisensory Integration: Somatosensory Speed Trumps Visual Accuracy during Feedback Control
Abstract
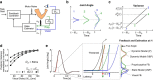
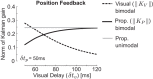
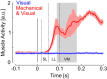
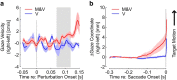
Recent advances in movement neuroscience have consistently highlighted that the nervous system performs sophisticated feedback control over very short time scales (<100 ms for upper limb). These observations raise the important question of how the nervous system processes multiple sources of sensory feedback in such short time intervals, given that temporal delays across sensory systems such as vision and proprioception differ by tens of milliseconds. Here we show that during feedback control, healthy humans use dynamic estimates of hand motion that rely almost exclusively on limb afferent feedback even when visual information about limb motion is available. We demonstrate that such reliance on the fastest sensory signal during movement is compatible with dynamic Bayesian estimation. These results suggest that the nervous system considers not only sensory variances but also temporal delays to perform optimal multisensory integration and feedback control in real-time.
Significance statement: Numerous studies have demonstrated that the nervous system combines redundant sensory signals according to their reliability. Although very powerful, this model does not consider how temporal delays may impact sensory reliability, which is an important issue for feedback control because different sensory systems are affected by different temporal delays. Here we show that the brain considers not only sensory variability but also temporal delays when integrating vision and proprioception following mechanical perturbations applied to the upper limb. Compatible with dynamic Bayesian estimation, our results unravel the importance of proprioception for feedback control as a consequence of the shorter temporal delays associated with this sensory modality.
Keywords: decision making; motor control; multisensory integration; state estimation.
Copyright © 2016 the authors 0270-6474/16/368598-14$15.00/0.
Figures

Similar articles
-
Different Sensory Information Is Used for State Estimation when Stationary or Moving.eNeuro. 2024 Sep 4;11(9):ENEURO.0357-23.2024. doi: 10.1523/ENEURO.0357-23.2024. Print 2024 Sep. eNeuro. 2024. PMID: 39147580 Free PMC article.
-
A perspective on multisensory integration and rapid perturbation responses.Vision Res. 2015 May;110(Pt B):215-22. doi: 10.1016/j.visres.2014.06.011. Epub 2014 Jul 9. Vision Res. 2015. PMID: 25014401 Review.
-
Using proprioception to control ongoing actions: dominance of vision or altered proprioceptive weighing?Exp Brain Res. 2018 Jul;236(7):1897-1910. doi: 10.1007/s00221-018-5258-7. Epub 2018 Apr 25. Exp Brain Res. 2018. PMID: 29696313
-
Intention tremor and deficits of sensory feedback control in multiple sclerosis: a pilot study.J Neuroeng Rehabil. 2014 Dec 19;11:170. doi: 10.1186/1743-0003-11-170. J Neuroeng Rehabil. 2014. PMID: 25526770 Free PMC article.
-
Visuomotor adaptation and proprioceptive recalibration.J Mot Behav. 2012;44(6):435-44. doi: 10.1080/00222895.2012.659232. J Mot Behav. 2012. PMID: 23237466 Review.
Cited by
-
Dissociable Effects of Urgency and Evidence Accumulation during Reaching Revealed by Dynamic Multisensory Integration.eNeuro. 2024 Dec 9;11(12):ENEURO.0262-24.2024. doi: 10.1523/ENEURO.0262-24.2024. Print 2024 Dec. eNeuro. 2024. PMID: 39542732 Free PMC article.
-
A bicycle can be balanced by stochastic optimal feedback control but only with accurate speed estimates.PLoS One. 2023 Feb 27;18(2):e0278961. doi: 10.1371/journal.pone.0278961. eCollection 2023. PLoS One. 2023. PMID: 36848331 Free PMC article.
-
Different sensory information is used for state estimation when stationary or moving.bioRxiv [Preprint]. 2024 Jun 29:2023.09.01.555979. doi: 10.1101/2023.09.01.555979. bioRxiv. 2024. Update in: eNeuro. 2024 Sep 4;11(9):ENEURO.0357-23.2024. doi: 10.1523/ENEURO.0357-23.2024. PMID: 37732193 Free PMC article. Updated. Preprint.
-
Visual Feedback Processing of the Limb Involves Two Distinct Phases.J Neurosci. 2019 Aug 21;39(34):6751-6765. doi: 10.1523/JNEUROSCI.3112-18.2019. Epub 2019 Jul 15. J Neurosci. 2019. PMID: 31308095 Free PMC article.
-
Increased muscle coactivation is linked with fast feedback control when reaching in unpredictable visual environments.iScience. 2024 Oct 16;27(11):111174. doi: 10.1016/j.isci.2024.111174. eCollection 2024 Nov 15. iScience. 2024. PMID: 39524350 Free PMC article.
References
-
- Anderson BDO, Moore JD. Optimal filtering. Engelwood Cliffs, New Jersey: Prentice-Hall; 1979.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical
