Estimating the Effective Population Size from Temporal Allele Frequency Changes in Experimental Evolution

Abstract

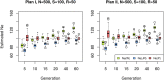
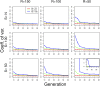
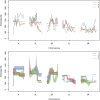
The effective population size ([Formula: see text]) is a major factor determining allele frequency changes in natural and experimental populations. Temporal methods provide a powerful and simple approach to estimate short-term [Formula: see text] They use allele frequency shifts between temporal samples to calculate the standardized variance, which is directly related to [Formula: see text] Here we focus on experimental evolution studies that often rely on repeated sequencing of samples in pools (Pool-seq). Pool-seq is cost-effective and often outperforms individual-based sequencing in estimating allele frequencies, but it is associated with atypical sampling properties: Additional to sampling individuals, sequencing DNA in pools leads to a second round of sampling, which increases the variance of allele frequency estimates. We propose a new estimator of [Formula: see text] which relies on allele frequency changes in temporal data and corrects for the variance in both sampling steps. In simulations, we obtain accurate [Formula: see text] estimates, as long as the drift variance is not too small compared to the sampling and sequencing variance. In addition to genome-wide [Formula: see text] estimates, we extend our method using a recursive partitioning approach to estimate [Formula: see text] locally along the chromosome. Since the type I error is controlled, our method permits the identification of genomic regions that differ significantly in their [Formula: see text] estimates. We present an application to Pool-seq data from experimental evolution with Drosophila and provide recommendations for whole-genome data. The estimator is computationally efficient and available as an R package at https://github.com/ThomasTaus/Nest.

Keywords: Pool-seq; effective population size; experimental evolution; genetic drift.

Figure 1

Two-step sampling in experimental evolution with Drosophila. In E&R studies, populations are propagated at a census size N defined by the experimenter, which is in general larger than the effective population size $N_{\mathrm{e}}.$ Using temporal methods, $N_{\mathrm{e}}$ can be estimated from the variance in allele frequency between samples taken t generations apart. To get an accurate representation of allele frequencies in population genetic studies, a large number of individuals $S_j$ ($j\in \left\{0,t\right\}$) are sampled and pooled. Sampling can take place according to sampling plan I or II based on the mode of reproduction. Pooled samples are then subjected to high-throughput sequencing. Sequenced reads are subsequently aligned to the reference genome (shown at the bottom). We represent pool sequencing by an additional sampling step (called sampling step 2). We correct for both sampling steps when estimating $N_{\mathrm{e}}$ in pooled samples. Additionally, we take into account variable coverage levels across the genome (coverage $R_{ij}$ for site i at $T=j,$ $j\in \left\{0,t\right\}$) when correcting for the variance coming from sequencing.

Figure 2

Effective population size estimated with different methods. Sixty generations of Wright–Fisher neutral evolution with $N_{\mathrm{e}}=100$ diploid individuals were simulated for n = 2000 unlinked loci (SNPs). Prior to sampling, the population was increased to a census size of $N=500$ individuals at each generation. At the starting population and at each indicated time point a sample was taken to create a pool of $S=100$ individuals. The pool was sequenced to an average coverage of $R=50$ and $N_{\mathrm{e}}$ was estimated on the resulting data set by separately contrasting allele frequencies at generation 0 to each of the evolved generations denoted on the x-axis, using $N_{\mathrm{e}}\left(P\right),$ $N_{\mathrm{e}}\left(W\right)$ (Waples 1989), and $N_{\mathrm{e}}\left(JR\right)$ (Jorde and Ryman 2007). Each box represents results from 100 simulations with identical parameters. The dashed gray line shows the true value of $N_{\mathrm{e}}.$ Data are simulated under plan I assumptions and the results of plan I and II estimators are shown in the left and right panels, respectively.

Figure 3

Coefficient of variation of $N_{\mathrm{e}}\left(P\right)$ under plan I for various parameter values. Neutral Wright–Fisher simulations were performed with various combinations of the parameters: effective population size ($N_{\mathrm{e}}=100,\hspace{0.5em}500,\hspace{0.5em}1000$ diploid individuals), pool size ($S=100,50$), and coverage ($R=150,\hspace{0.5em}100,\hspace{0.5em}50$). $N_{\mathrm{e}}$ was estimated with $N_{\mathrm{e}}\left(P\right)$ under plan I, using $n=2000$ SNPs. $S=N$ indicates scenarios when the whole population is sequenced as a single pool. For all simulations, we assumed $N=N_{\mathrm{e}}.$ Each value is calculated over 100 simulations. When the coefficient of variation exceeds one, the inset shows the actual value.

Figure 4

Effect of the number of SNPs used for estimating $N_{\mathrm{e}}.$ The effective population size is estimated using $N_{\mathrm{e}}\left(P\right)$ plan I on simulated data with $N_{\mathrm{e}}=N=100.$ A total number of $S=100$ individuals are pooled and sequenced at a mean coverage of $R=50.$ Based on 100 simulation runs, $N_{\mathrm{e}}$ is estimated using different numbers of SNPs at multiple time points.

Figure 5

Influence of the starting allele frequency distribution on $N_{\mathrm{e}}\left(P\right)$ under plan I. A comparison between uniform and Beta(0.2, 0.2)-distributed (neutral) starting allele frequencies is shown. The simulation parameters match those of the genome-wide simulations in Figure 6.

Figure 6

Effect of linkage disequilibrium on ${\widehat{N}}_{\mathrm{e}}.$ The effect of linkage disequilibrium on our estimator was evaluated based on a whole-genome forward simulation with recombination using the software MimicrEE (Kofler and Schlötterer 2014). Three sets of simulations were performed with different rates of recombination: high, normal, and no recombination. For each parameter setup, a genome-wide simulation is replicated 10 times. The effective population size was estimated with $N_{\mathrm{e}}\left(P\right)$ (plan I) in nonoverlapping windows of n = 10,000 SNPs for each replicate. The box plots show the distribution of $N_{\mathrm{e}}$ estimates across replicates and windows.

Figure 7

Genome-wide ${\widehat{N}}_{\mathrm{e}}$ from an E&R study with D. melanogaster. $N_{\mathrm{e}}$ is estimated based on the allele frequency changes between founder and evolved populations at generation 59 (Franssen et al. 2015). In the top panel, we show genome-wide estimates calculated with $N_{\mathrm{e}}\left(P\right)$ (plan I), using $N=1000$ as census size and $S=500$ as pool size (Orozco-terWengel et al. 2012) and nonoverlapping windows of 10,000 SNPs. Chromosome-wide mean estimates across replicates are shown by the dashed lines and also calculated separately for each replicate in Table 1. DNA stretches with significantly different ${\widehat{N}}_{\mathrm{e}}$ are determined using the stepR software package (Frick et al. 2014) (bottom panel). Lower and upper $1-\alpha$ confidence bands are shown as shaded areas. α controls the error, i.e., the probability for overestimating the number of change points, and is calculated automatically as described in Frick et al. (2014). The colors indicate different biological replicates.