Mathematical modeling of gonadotropin-releasing hormone signaling
- PMID: 27544781
- PMCID: PMC5446263
- DOI: 10.1016/j.mce.2016.08.022
Mathematical modeling of gonadotropin-releasing hormone signaling
Abstract
Gonadotropin-releasing hormone (GnRH) acts via G-protein coupled receptors on pituitary gonadotropes to control reproduction. These are Gq-coupled receptors that mediate acute effects of GnRH on the exocytotic secretion of luteinizing hormone (LH) and follicle-stimulating hormone (FSH), as well as the chronic regulation of their synthesis. GnRH is secreted in short pulses and GnRH effects on its target cells are dependent upon the dynamics of these pulses. Here we overview GnRH receptors and their signaling network, placing emphasis on pulsatile signaling, and how mechanistic mathematical models and an information theoretic approach have helped further this field.
Keywords: ERK; GPCR; GnRH; Mathematical modeling; Mutual information; NFAT.
Copyright © 2016 The Authors. Published by Elsevier B.V. All rights reserved.
Figures
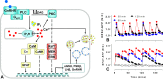
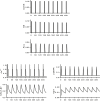



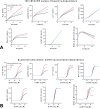


Comment in
-
Mathematical modeling of gonadotropin-releasing hormone signaling.Mol Cell Endocrinol. 2018 Jul 15;470:34-35. doi: 10.1016/j.mce.2017.09.034. Epub 2017 Oct 4. Mol Cell Endocrinol. 2018. PMID: 28987814 No abstract available.
-
Authors response to communication about mathematical modeling of gonadotropin-releasing hormone signaling.Mol Cell Endocrinol. 2018 Jul 15;470:36-37. doi: 10.1016/j.mce.2017.09.035. Epub 2017 Oct 4. Mol Cell Endocrinol. 2018. PMID: 28987815 No abstract available.
References
-
- Alon U. Network motifs: theory and experimental approaches. Nat. Rev. Genet. 2007;8:450–461. - PubMed
-
- Bedecarrats G.Y., Kaiser U.B. Differential regulation of gonadotropin subunit gene promoter activity by pulsatile gonadotropin-releasing hormone (GnRH) in perifused L beta T2 cells: role of GnRH receptor concentration. Endocrinology. 2003;144:1802–1811. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Miscellaneous

