On standardized relative survival
- PMID: 27554303
- PMCID: PMC5507182
- DOI: 10.1111/biom.12578
On standardized relative survival
Abstract
Cancer survival comparisons between cohorts are often assessed by estimates of relative or net survival. These measure the difference in mortality between those diagnosed with the disease and the general population. For such comparisons methods are needed to standardize cohort structure (including age at diagnosis) and all-cause mortality rates in the general population. Standardized non-parametric relative survival measures are evaluated by determining how well they (i) ensure the correct rank ordering, (ii) allow for differences in covariate distributions, and (iii) possess robustness and maximal estimation precision. Two relative survival families that subsume the Ederer-I, Ederer-II, and Pohar-Perme statistics are assessed. The aforementioned statistics do not meet our criteria, and are not invariant under a change of covariate distribution. Existing methods for standardization of these statistics are either not invariant to changes in the general population mortality or are not robust. Standardized statistics and estimators are developed to address the deficiencies. They use a reference distribution for covariates such as age, and a reference population mortality survival distribution that is recommended to approach zero with increasing age as fast as the cohort with the worst life expectancy. Estimators are compared using a breast-cancer survival example and computer simulation. The proposals are invariant and robust, and out-perform current methods to standardize the Ederer-II and Pohar-Perme estimators in simulations, particularly for extended follow-up.
Keywords: Cancer; Ederer-II; Epidemiology; Excess Hazards; Heterogeneity; Net Survival; Relative Survival; Robust Estimation; Standardization; Weighted Excess Hazards; Weighted Net Survival; Weighted Relative Survival.
© 2016 The Authors Biometrics published by Wiley Periodicals, Inc. on behalf of International Biometric Society.
Figures

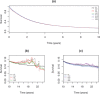

 ) and standard survival statistics (
,
) and standard survival statistics (
,  ; both with weights (9)) in the reference population are given; samples are from two cohort populations [1] and [2]. Net survival estimates are from PPa, traditional standardization applied to Pohar‐Perme estimation, and PPb which is Brenner standardization from (8). The standardized survival estimates and with weights (9) are labeled, respectively, R1S and R2S.
; both with weights (9)) in the reference population are given; samples are from two cohort populations [1] and [2]. Net survival estimates are from PPa, traditional standardization applied to Pohar‐Perme estimation, and PPb which is Brenner standardization from (8). The standardized survival estimates and with weights (9) are labeled, respectively, R1S and R2S.References
-
- Andersen, P. K. , Borgan, O. , Gill, R. D. , and Keiding, N. (1996). Statistical Models Based on Counting Processes. New York: Springer.
-
- Bickel, P. J. and Lehmann, E. L. (1975). Descriptive statistics for nonparametric models II. Location. The Annals of Statistics 3, 1045–1069.
-
- Brenner, H. , Arndt, V. , Gefeller, O. , and Hakulinen, T. (2004). An alternative approach to age adjustment of cancer survival rates. European Journal of Cancer 40, 2317–2322. - PubMed
-
- Brenner, H. and Hakulinen, T. (2003). On crude and age‐adjusted relative survival rates. Journal of Clinical Epidemiology 56, 1185–1191. - PubMed
-
- Corazziari, I. , Quinn, M. , and Capocaccia, R. (2004). Standard cancer patient population for age standardising survival ratios. European Journal of Cancer 40, 2307–2316. - PubMed
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

