Molecular graph convolutions: moving beyond fingerprints
- PMID: 27558503
- PMCID: PMC5028207
- DOI: 10.1007/s10822-016-9938-8
Molecular graph convolutions: moving beyond fingerprints
Abstract
Molecular "fingerprints" encoding structural information are the workhorse of cheminformatics and machine learning in drug discovery applications. However, fingerprint representations necessarily emphasize particular aspects of the molecular structure while ignoring others, rather than allowing the model to make data-driven decisions. We describe molecular graph convolutions, a machine learning architecture for learning from undirected graphs, specifically small molecules. Graph convolutions use a simple encoding of the molecular graph-atoms, bonds, distances, etc.-which allows the model to take greater advantage of information in the graph structure. Although graph convolutions do not outperform all fingerprint-based methods, they (along with other graph-based methods) represent a new paradigm in ligand-based virtual screening with exciting opportunities for future improvement.
Keywords: Artificial neural networks; Deep learning; Machine learning; Molecular descriptors; Virtual screening.
Figures


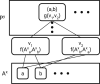
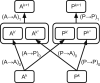
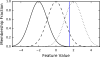
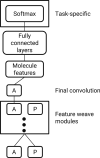
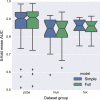

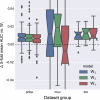


References
-
- Abadi M, Agarwal A, Barham P, Brevdo E, Chen Z, Citro C, Corrado GS, Davis A, Dean J, Devin M, et al. TensorFlow: large-scale machine learning on heterogeneous systems. Software. 2015 http://tensorflow.org.
-
- Ballester PJ, Richards WG. Ultrafast shape recognition to search compound databases for similar molecular shapes. J Comput Chem. 2007;28(10):1711–1723. - PubMed
-
- Bruna J, Zaremba W, Szlam A, LeCun Y. Spectral networks and locally connected networks on graphs. arXiv. 2013:1312–6203.
-
- Carhart RE, Smith DH, Venkataraghavan R. Atom pairs as molecular features in structure-activity studies: definition and applications. J Chem Inf Comput Sci. 1985;25(2):64–73.
-
- Dahl G. Deep learning how I did it: Merck 1st place interview. 2012 http://blog.kaggle.com/2012/11/01/deep-learning-how-i-did-it-merck-1st-p....
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

