Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
Comment
. 2016 Aug 25;12(8):e1005679.
doi: 10.1371/journal.ppat.1005679. eCollection 2016 Aug.

Insufficient Evidence for Rare Activation of Latent HIV in the Absence of Reservoir-Reducing Interventions

Alison L Hill  1 , Daniel I S Rosenbloom  2 , Janet D Siliciano  3 , Robert F Siliciano  3   4
Affiliations
Comment

Insufficient Evidence for Rare Activation of Latent HIV in the Absence of Reservoir-Reducing Interventions

Alison L Hill et al. PLoS Pathog. .
No abstract available

PubMed Disclaimer

Conflict of interest statement

The authors have declared that no competing interests exist.

Figures

Fig 1
Fig 1. Alternatives to the Pinkevych et al. interpretation of rebound dynamics.
Time-to-rebound data can be explained equally well by frequent reactivation in a realistically heterogeneous cohort (Fig 1B–D) as by rare reactivation in a homogeneous population (Fig 1A). Top row: Observed rebound times in “Cohort 3” [8] and best fits from models described in text. Bottom row: Representative rebound trajectories from 10 participants randomly simulated with the best-fit parameters for each model. (A) The best-fit model derived by Pinkevych et al. All participants are identical, with k = 1/(5.1 days). We fixed r = 0.4/day and fit V 0 = 4 c/ml. (B) Allowing interperson variation in growth rate, r. We assumed the population distribution of r was log10-normal with log10-mean μr = –0.4 (10μr = 0.4/day) [,,–12] and fit the log10-standard deviation σr = 0.2 (consistent with [1,12]). We fixed k = 4 cells/day and fit V 0 = 0.15 c/ml. (C) Allowing interperson variation in the activation rate, k. We assumed the population distribution of k was log10-normal with μk = 0.6 (10μk = 4 cells/day) [1,12] and fit the log10-standard deviation σk = 0.55 (less than estimated in [1,12], similar to [13]). We fixed r = 0.4/day and fit V 0 = 0.15 c/ml. (D) Allowing interperson variation in both activation rate and growth rate. We assumed the population distribution of k and r were log10-normal. Taking μr and σr to be –0.4 (10μr = 0.4/day) and 0.1 and μk = 0.6 (10μk = 4 cells/day), we fit σk = 0.45. We additionally fit V 0 = 0.15 c/ml. For all simulations, the definition of viral rebound was set to 50 c/ml and the drug washout time to zero. In general, only two model parameters are identifiable from the cohort data and so the choice of which were fixed and which were fit was arbitrary. Higher V 0 values paired with lower r values could fit equally well, as could either paired with higher drug washout times. Note that in simulating the Pinkevych et al. model, we allow for the possibility that multiple reactivating cells contribute to viral rebound, as otherwise the model cannot be used to describe higher activation rates.
Fig 2
Fig 2. Alternatives to the Pinkevych et al. interpretation of founder virus ratios.
Viral genotyping during early rebound in six participants in cohort 4 [9,14] identified multiple unique viral strains contributing to rebound and characterized their relative frequencies. Ratios were defined as the number of sequences from one strain divided by the number of sequences from the next most prevalent strain. The cumulative distribution function (CDF) for the frequency of each ratio, with all participant data combined, is shown (solid black line). Pinkevych et al. used maximum likelihood estimation to determine the activation rate k that best explains this distribution, assuming all strains start at the same level and grow at the same rate once reactivated. The CDF for the ratios using their estimated activation rate (k = 1/(3.6 days)) is shown (dashed blue line). Alternatively, we assume that strains activate at the same time (high activation rate) but that the growth rates of individual strains are normally distributed with unknown mean and variance. Using maximum likelihood estimation, we infer that an interstrain standard deviation in growth rate of 0.09/day can explain the observed clone ratios (dotted red line). This estimate increases to 0.19 under alternate assumptions about the sampling procedure (see S1 Text).
See this image and copyright information in PMC

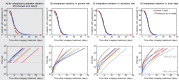
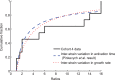
Comment in

Comment on

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Hill AL, Rosenbloom DIS, Fu F, Nowak MA, Siliciano RF. Predicting the outcomes of treatment to eradicate the latent reservoir for HIV-1. Proc Natl Acad Sci. 2014;111: 13475–13480. 10.1073/pnas.1406663111 - DOI - PMC - PubMed
    1. Pinkevych M, Cromer D, Tolstrup M, Grimm AJ, Cooper DA, Lewin SR, et al. HIV Reactivation from Latency after Treatment Interruption Occurs on Average Every 5–8 Days—Implications for HIV Remission. PLoS Pathog. 2015;11: e1005000 10.1371/journal.ppat.1005000 - DOI - PMC - PubMed
    1. Pennings PS. Standing Genetic Variation and the Evolution of Drug Resistance in HIV. PLoS Comput Biol. 2012;8: e1002527 10.1371/journal.pcbi.1002527 - DOI - PMC - PubMed
    1. Rosenbloom DIS, Hill AL, Rabi SA, Siliciano RF, Nowak MA. Antiretroviral dynamics determines HIV evolution and predicts therapy outcome. Nat Med. 2012;18: 1378–1385. 10.1038/nm.2892 - DOI - PMC - PubMed
    1. Ribeiro RM. In vivo dynamics of T cell activation, proliferation, and death in HIV-1 infection: Why are CD4+ but not CD8+ T cells depleted? Proc Natl Acad Sci. 2002;99: 15572–15577. 10.1073/pnas.242358099 - DOI - PMC - PubMed

Publication types

LinkOut - more resources