Modelling the impact and control of an infectious disease in a plant nursery with infected plant material inputs

Abstract

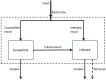
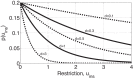
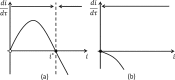
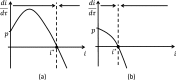
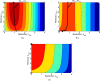
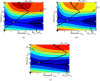
The ornamental plant trade has been identified as a key introduction pathway for plant pathogens. Establishing effective biosecurity measures to reduce the risk of plant pathogen outbreaks in the live plant trade is therefore important. Management of invasive pathogens has been identified as a weakest link public good, and thus is reliant on the actions of individual private agents. This paper therefore provides an analysis of the impact of the private agents' biosecurity decisions on pathogen prevention and control within the plant trade. We model the impact that an infectious disease has on a plant nursery under a constant pressure of potentially infected input plant materials, like seeds and saplings, where the spread of the disease reduces the value of mature plants. We explore six scenarios to understand the influence of three key bioeconomic parameters; the disease's basic reproductive number, the loss in value of a mature plant from acquiring an infection and the cost-effectiveness of restriction. The results characterise the disease dynamics within the nursery and explore the trade-offs and synergies between the optimal level of efforts on restriction strategies (actions to prevent buying infected inputs), and on removal of infected plants in the nursery. For diseases that can be easily controlled, restriction and removal are substitutable strategies. In contrast, for highly infectious diseases, restriction and removal are often found to be complementary, provided that restriction is cost-effective and the optimal level of removal is non-zero.

Keywords: Bioeconomic model; Optimal control; Plant disease; Plant nursery model.

Fig. 1

A transfer diagram representing the disease dynamics within the nursery.

Fig. 2

Proportion of infected plant inputs, p(u_ins), where p(u_ins) = (a − b)exp(−du_ins) + b with a = 0.2, b = 0 and various of values of d. The solid lines are values used in Scenarios found in Section 3.

Fig. 3

Perfect restriction (p = 0). (a) If $R_0^{\mathrm{rem}}=\frac{R_0}{1+u_{\mathrm{rem}}}>1$, then the prevalence equation is negative for all positive prevalence. There is one non-negative steady state, i^* = 0, which is stable. then the prevalence equation is a form of logistic growth. There are two steady states (where $\frac{\mathrm{di}}{d\tau }$), i^* = 0 and $i^{*}=1-\frac{1}{R_0^{\mathrm{rem}}}$. i = 0 is unstable and that for the region between i = 0 and $i=1-\frac{1}{R_0^{\mathrm{rem}}}$, $\frac{\mathrm{di}}{d\tau }>0$ and thus disease prevalence will increase over time (represented by the arrow at the top). (b) If $R_0^{\mathrm{rem}}<1$, then the prevalence equation is negative for all positive prevalence. There is one non-negative steady state, i^* = 0, which is stable. Note that when u_rem = 0, $R_0^{\mathrm{rem}}=R_0$.

Fig. 4

Imperfect restriction (p > 0). (a) $R_0^p=\frac{R_0}{1+u_{\mathrm{rem}}(1-p)}>1$ and (b) $R_0^p=\frac{R_0}{1+u_{\mathrm{rem}}(1-p)}<1$. For both figures have only one steady state that is stable; there is no disease-free steady state unlike the case with p = 0.

Fig. 5

Contour plots of Q with respect to both removal and restriction for (a) Scenario 1a, (b) Scenario 1b and (c) Scenario 1c. Red regions are the regions of lowest costs whereas blue regions signify highest costs. The black solid line represents MB_ins=MC_ins (there are no lines for removal in this Scenario). Black dots are local minima, white dots are local maxima and grey dots are saddle points (points on the right boundary are local maxima/saddle point if we limit u_ins to regions in these figures). R₀, L and d are given in Table 1. Other parameters: C = 10, a = 0.2 and b = 0. (For interpretation of the references to colour in this figure, the reader is referred to the web version of this article.)

Fig. 6

Contour plots of profit Q with respect to both removal and restriction for (a) Scenario 2a, (b) Scenario 2b and (c) Scenario 2c. Red regions are the regions of lowest costs whereas blue regions signify highest costs. The black lines represent MB_ins=MC_ins and MB_rem=MC_rem whereas the grey line represents the values of (u_ins, u_rem) that correspond to $R_0^p=1$. The dots have the same meaning as Fig. 5(a). R₀, L and d are given in Table 1. Other parameters are the same as Fig. 5. (For interpretation of the references to colour in this figure, the reader is referred to the web version of this article.)