Adaptive anisotropic diffusion for noise reduction of phase images in Fourier domain Doppler optical coherence tomography

Abstract

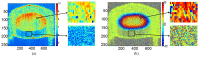
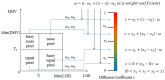
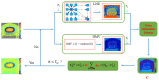
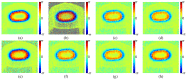
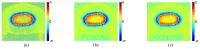
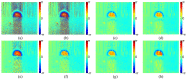
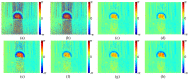
Phase image in Fourier domain Doppler optical coherence tomography offers additional flow information of investigated samples, which provides valuable evidence towards accurate medical diagnosis. High quality phase images are thus desirable. We propose a noise reduction method for phase images by combining a synthetic noise estimation criteria based on local noise estimator (LNE) and distance median value (DMV) with anisotropic diffusion model. By identifying noise and signal pixels accurately and diffusing them with different coefficients respectively and adaptive iteration steps, we demonstrated the effectiveness of our proposed method in both phantom and mouse artery images. Comparison with other methods such as filtering method (mean, median filtering), wavelet method, probabilistic method and partial differential equation based methods in terms of peak signal-to-noise ratio (PSNR), equivalent number of looks (ENL) and contrast-to-noise ratio (CNR) showed the advantages of our method in reserving image energy and removing noise.

Keywords: (030.4280) Noise in imaging systems; (100.0100) Image processing; (110.4500) Optical coherence tomography.

Fig. 1

OCT image of a phantom transparent plastic tube: (a) intensity image. (b) phase image. Two regions are selected and enlarged in the right side.

Fig. 2

The noise estimation criteria. DMV and LNE denote numerical value on one dimension. Max(DMV), Max(LNE) are the maximum value of DMV, LNE. T₁,T₂ are two threshold values corresponding to DMV and LNE.

Fig. 3

The implement filter process for a image.

Fig. 4

The processed results (cropped to 258 by 784 pixels) using different methods. (a) reference standard phase image. (b) PM diffusion with the same iteration number as (h) . (c) NCDF method with the same parameters as [20]. (d) mean filter. (e) median filter with w = 3. (f) wavelet method with matlab function: ddencmp, wdencmp . (g) Bayesian method with same parameters as [35]. (h) our method with parameters $\text{r},T_l,T_1,T_2,x_1,x_2,x_3$, which will be explained in subsection 3.4.

Fig. 5

Eight regions of interest and one background region are marked in the filtering results (258 x 784 pixels). (a) phase image with noise. (b) PM diffusion. (c) NCDF method. (d) mean filter. (e) median filter. (f) wavelet method. (g) Bayesian method. (h) our method.

Fig. 6

The results comparision of the filter process. (a) iteration error curve. (b) a red line is marked in the phase image. (c) comparision of curves for red line in (b) using different methods.

Fig. 7

Results for different diffusivity. (a) LNE is used as diffusivity. The maximum PSNR is 11.68 dB. (b) DMV is used as diffusivity. The maximum PSNR is 17 dB. (c) Our diffusivity. The maximum PSNR is 18 dB.

Fig. 8

The optimization process of parameters by the genetic algorithm. Population size is 50, MAXGEN is 125, individual length is 20, cross probability is 0.7 and mutative probability is 0.01. (a) The outline of the optimization process. (b) The change of PSNR in the optimization process.

Fig. 9

The processed results (200 x 999 pixels) using different methods. (a) phase image with noise, which is 7 frame phase image. (b) PM diffusion with 23 iteration. (c) NCDF method with the same parameters as [20]. (d) mean filter. (e) median filter with w = 3. (f) wavelet method with matlab function: ddencmp, wdencmp . (g) Bayesian method with same parameters as [35]. (h) our method with the iteration number is 23.

Fig. 10

Four regions of interest and one background region are marked in the filtering results (200 x 999 pixels). (a) phase image with noise. (b) PM diffusion. (c) NCDF method. (d) mean filter. (e) median filter. (f) wavelet method. (g) Bayesian method. (h) our method.

Fig. 11

The processed results (200 x 999 pixels) using different methods. (a) phase image with noise, which is 19 frame phase image. (b) PM diffusion with 23 iteration. (c) NCDF method with the same parameters as [20]. (d) mean filter. (e) median filter with w = 3. (f) wavelet method with matlab function: ddencmp, wdencmp . (g) Bayesian method with same parameters as [35]. (h) our method with iteration number is 23

Fig. 12

Four regions of interest and one background region are marked in the filtering results (200 x 999 pixels). (a) phase image with noise. (b) PM diffusion. (c) NCDF method. (d) mean filter. (e) median filter. (f) wavelet method. (g) Bayesian method. (h) our method.

Fig. 13

The processed results (200 x 999 pixels) using different methods. (a) phase image with noise, which is 23 frame phase image. (b) PM diffusion with 23 iteration. (c) NCDF method with the same parameters as [20]. (d) mean filter. (e) median filter with w = 3. (f) wavelet method with matlab function: ddencmp, wdencmp . (g) Bayesian method with same parameters as [35]. (h) our method with iteration number is 23.