Validation and optimization of hypercapnic-calibrated fMRI from oxygen-sensitive two-photon microscopy

Abstract

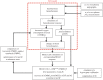
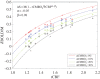
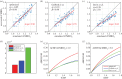
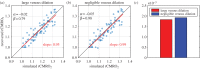
Hypercapnic-calibrated fMRI allows the estimation of the relative changes in the cerebral metabolic rate of oxygen (rCMRO2) from combined BOLD and arterial spin labelling measurements during a functional task, and promises to permit more quantitative analyses of brain activity patterns. The estimation relies on a macroscopic model of the BOLD effect that balances oxygen delivery and consumption to predict haemoglobin oxygenation and the BOLD signal. The accuracy of calibrated fMRI approaches has not been firmly established, which is limiting their broader adoption. We use our recently developed microscopic vascular anatomical network model in mice as a ground truth simulator to test the accuracy of macroscopic, lumped-parameter BOLD models. In particular, we investigate the original Davis model and a more recent heuristic simplification. We find that these macroscopic models are inaccurate using the originally defined parameters, but that the accuracy can be significantly improved by redefining the model parameters to take on new values. In particular, we find that the parameter α that relates cerebral blood-volume changes to cerebral blood-flow changes is significantly smaller than typically assumed and that the optimal value changes with magnetic field strength. The results are encouraging in that they support the use of simple BOLD models to quantify BOLD signals, but further work is needed to understand the physiological interpretation of the redefined model parameters.This article is part of the themed issue 'Interpreting BOLD: a dialogue between cognitive and cellular neuroscience'.

Keywords: Monte Carlo simulations; calibrated fMRI; cerebral metabolism; two-photon microscopy.

Figure 1.

Schematic overview of the simulations performed. The VAN model describes oxygen advection and diffusion in real vascular networks in shown in red.

Figure 2.

Three-dimensional rendering of the six vascular stacks acquired with two-photon microscopy. Each of these vascular stacks was subsequently used in a VAN model, and the MRI signal was computed with Monte Carlo simulations for each to these VAN models.

Figure 3.

BOLD-CBF isometabolic contour plots illustrating the 72 simulations (three dilations ×4 CMRO₂ increases ×6 VANs). Each symbol represents an individual animal or VAN. Different levels of CMRO₂ increases are illustrated by different colours. It is to note that the same level of arterial dilation (10%, 20% and 30%) produces different levels of CBF increase for each animal. The values shown (α =−0.05 and β = 0.98) are the ones that minimized the mean square error between the simulated rCMRO₂ and the recovered macroscopic rCMRO₂ using the Davis model. Solid lines illustrate the theoretical BOLD signal from the Davis model for (α =−0.05 and β = 0.98), i.e. the best fit of the Davis model to the simulated data (individual symbols).

Figure 4.

Validation and optimization of the Davis model. (a) Optimization of the free parameter α and β. The values shown (α =−0.05 and β = 0.98) are the ones that minimized the mean-squared error between the simulated microscopic rCMRO₂ and the recovered macroscopic rCMRO₂. The values for each individual simulations are displayed on a scatter plot of the recovered rCMRO₂ versus the simulated rCMRO₂. (b) Scatter plot of recovered versus simulated rCMRO₂ by using the values for the free parameters proposed by Griffeth et al. [28]. (c) Scatter plot of recovered versus simulated rCMRO₂ by using the values for the free parameters originally proposed by Davis et al. [7]. (d) Mean-squared error between the recovered and the simulated rCMRO₂ for three different sets of the free parameters: our new optimized values, Griffeth et al. [28] and Davis et al. [7]. (e) Plot of the BOLD responses obtained from different increases in CBF with each of the three sets of values for the free parameter. A flow-metabolic coupling ratio of 2 was assumed. (f) Same as (e) but with flow-metabolic coupling of 3 assumed.

Figure 5.

Effect of a larger venous dilation. (a) Optimization of the free parameter α and β for VAN simulations in which the veins were forced to dilate according to a Grubb exponent of 0.38. In this case, the optimal values obtained were α = −0.02 and β = 0.79. (b) Scatter plot of the recovered rCMRO₂ versus the simulated rCMRO₂ by simulating the BOLD response with the forced venous dilation but by using the optimal values computed with negligible venous dilation (i.e. α = −0.05 and β = 0.98) rather than the ones optimized for the large venous dilation (α = −0.02 and β = 0.79). (c) Mean-squared error between the simulated and the recovered rCMRO₂ obtained using each set of free parameters. In each case, the BOLD response was simulated by forcing a large venous dilation in the VAN. The only difference is the value used as free parameters in the Davis model.

Figure 6.

Accuracy of a simplified heuristic BOLD model (Griffeth [29]). (a) Optimization of the sole free parameter (α_v = −0.05) of the heuristic model using the same procedure illustrated in figure 1. (b) Replication of figure 4b for comparison purpose. (c) Mean-squared error between the simulated rCMRO₂ and the recovered rCMRO₂ using the Davis model with our new optimized parameters (α = −0.05 and β = 0.98) and the heuristic model with (α_v = −0.05).