Experimental Design for Stochastic Models of Nonlinear Signaling Pathways Using an Interval-Wise Linear Noise Approximation and State Estimation
- PMID: 27583802
- PMCID: PMC5008843
- DOI: 10.1371/journal.pone.0159902
Experimental Design for Stochastic Models of Nonlinear Signaling Pathways Using an Interval-Wise Linear Noise Approximation and State Estimation
Abstract
Background: Computational modeling is a key technique for analyzing models in systems biology. There are well established methods for the estimation of the kinetic parameters in models of ordinary differential equations (ODE). Experimental design techniques aim at devising experiments that maximize the information encoded in the data. For ODE models there are well established approaches for experimental design and even software tools. However, data from single cell experiments on signaling pathways in systems biology often shows intrinsic stochastic effects prompting the development of specialized methods. While simulation methods have been developed for decades and parameter estimation has been targeted for the last years, only very few articles focus on experimental design for stochastic models.
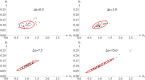
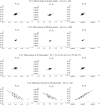
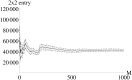
Methods: The Fisher information matrix is the central measure for experimental design as it evaluates the information an experiment provides for parameter estimation. This article suggest an approach to calculate a Fisher information matrix for models containing intrinsic stochasticity and high nonlinearity. The approach makes use of a recently suggested multiple shooting for stochastic systems (MSS) objective function. The Fisher information matrix is calculated by evaluating pseudo data with the MSS technique.
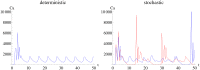
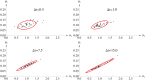
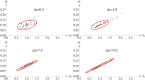
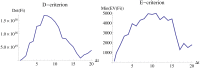
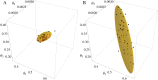
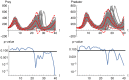
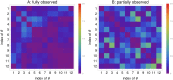
Results: The performance of the approach is evaluated with simulation studies on an Immigration-Death, a Lotka-Volterra, and a Calcium oscillation model. The Calcium oscillation model is a particularly appropriate case study as it contains the challenges inherent to signaling pathways: high nonlinearity, intrinsic stochasticity, a qualitatively different behavior from an ODE solution, and partial observability. The computational speed of the MSS approach for the Fisher information matrix allows for an application in realistic size models.
Conflict of interest statement
The author has declared that no competing interests exist.
Figures
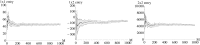
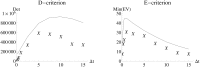






Similar articles
-
Reconstructing the hidden states in time course data of stochastic models.Math Biosci. 2015 Nov;269:117-29. doi: 10.1016/j.mbs.2015.08.015. Epub 2015 Sep 9. Math Biosci. 2015. PMID: 26363082
-
Comparison of approaches for parameter estimation on stochastic models: Generic least squares versus specialized approaches.Comput Biol Chem. 2016 Apr;61:75-85. doi: 10.1016/j.compbiolchem.2015.10.003. Epub 2015 Dec 17. Comput Biol Chem. 2016. PMID: 26826353
-
Deterministic inference for stochastic systems using multiple shooting and a linear noise approximation for the transition probabilities.IET Syst Biol. 2015 Oct;9(5):181-92. doi: 10.1049/iet-syb.2014.0020. IET Syst Biol. 2015. PMID: 26405142 Free PMC article.
-
A comparison of deterministic and stochastic approaches for sensitivity analysis in computational systems biology.Brief Bioinform. 2020 Mar 23;21(2):527-540. doi: 10.1093/bib/bbz014. Brief Bioinform. 2020. PMID: 30753281 Review.
-
Estimation methods for heterogeneous cell population models in systems biology.J R Soc Interface. 2018 Oct 31;15(147):20180530. doi: 10.1098/rsif.2018.0530. J R Soc Interface. 2018. PMID: 30381346 Free PMC article. Review.
Cited by
-
Supercritical CO2 Extraction of Extracted Oil from Pistacia lentiscus L.: Mathematical Modeling, Economic Evaluation and Scale-Up.Molecules. 2020 Jan 3;25(1):199. doi: 10.3390/molecules25010199. Molecules. 2020. PMID: 31947791 Free PMC article.
-
Comprehensive Review of Models and Methods for Inferences in Bio-Chemical Reaction Networks.Front Genet. 2019 Jun 14;10:549. doi: 10.3389/fgene.2019.00549. eCollection 2019. Front Genet. 2019. PMID: 31258548 Free PMC article. Review.
-
The finite state projection based Fisher information matrix approach to estimate information and optimize single-cell experiments.PLoS Comput Biol. 2019 Jan 15;15(1):e1006365. doi: 10.1371/journal.pcbi.1006365. eCollection 2019 Jan. PLoS Comput Biol. 2019. PMID: 30645589 Free PMC article.
-
Optimal Design of Single-Cell Experiments within Temporally Fluctuating Environments.Complexity. 2020;2020:8536365. doi: 10.1155/2020/8536365. Epub 2020 Jun 13. Complexity. 2020. PMID: 32982137 Free PMC article.
References
-
- Gillespie DT. A General Method for Numerically Simulating the Stochastic Time Evolution of coupled Chemical Reactions. Journal of Computational Physics. 1976;22 (4):403–434. 10.1016/0021-9991(76)90041-3 - DOI
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources

