Evolution of Site-Selection Stabilizes Population Dynamics, Promotes Even Distribution of Individuals, and Occasionally Causes Evolutionary Suicide
- PMID: 27647007
- PMCID: PMC5039230
- DOI: 10.1007/s11538-016-0198-5
Evolution of Site-Selection Stabilizes Population Dynamics, Promotes Even Distribution of Individuals, and Occasionally Causes Evolutionary Suicide
Abstract
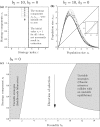
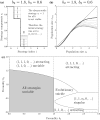
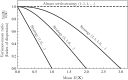
Species that compete for access to or use of sites, such as parasitic mites attaching to honey bees or apple maggots laying eggs in fruits, can potentially increase their fitness by carefully selecting sites at which they face little or no competition. Here, we systematically investigate the evolution of site-selection strategies among animals competing for discrete sites. By developing and analyzing a mechanistic and population-dynamical model of site selection in which searching individuals encounter sites sequentially and can choose to accept or continue to search based on how many conspecifics are already there, we give a complete characterization of the different site-selection strategies that can evolve. We find that evolution of site-selection stabilizes population dynamics, promotes even distribution of individuals among sites, and occasionally causes evolutionary suicide. We also discuss the broader implications of our findings and propose how they can be reconciled with an earlier study (Nonaka et al. in J Theor Biol 317:96-104, 2013) that reported selection toward ever higher levels of aggregation among sites as a consequence of site-selection.
Keywords: Adaptive dynamics; Evolution; Evolutionary suicide; First-principles derivation; Mechanistic modeling.
Figures




Similar articles
-
Evolutionary Suicide of Prey: Matsuda and Abrams' Model Revisited.Bull Math Biol. 2019 Nov;81(11):4778-4802. doi: 10.1007/s11538-018-0472-9. Epub 2018 Aug 17. Bull Math Biol. 2019. PMID: 30120688
-
The evolution of site-selection strategy during dispersal.J Theor Biol. 2017 Jul 21;425:11-22. doi: 10.1016/j.jtbi.2017.05.002. Epub 2017 May 4. J Theor Biol. 2017. PMID: 28478118
-
Why does invasion imply substitution? Beyond the paradigm of invasion fitness.J Math Biol. 2018 Nov;77(5):1493-1532. doi: 10.1007/s00285-018-1261-7. Epub 2018 Jul 2. J Math Biol. 2018. PMID: 29961929
-
Eco-evolutionary feedbacks, adaptive dynamics and evolutionary rescue theory.Philos Trans R Soc Lond B Biol Sci. 2013 Jan 19;368(1610):20120081. doi: 10.1098/rstb.2012.0081. Philos Trans R Soc Lond B Biol Sci. 2013. PMID: 23209163 Free PMC article. Review.
-
Toward an ecological synthesis: a case for habitat selection.Oecologia. 2003 Jun;136(1):1-13. doi: 10.1007/s00442-003-1241-4. Epub 2003 Apr 11. Oecologia. 2003. PMID: 12690550 Review.
References
-
- Allee WC, Emerson A, Park T, Schmidt K. Principles of animal ecology. Philadelphia: Saunders; 1949.
-
- Anazawa M. Bottom-up derivation of discrete-time population models with the Allee effect. Theor Popul Biol. 2009;75:56–67. - PubMed
-
- Anazawa M. The mechanistic basis of discrete-time population models: the role of resource partitioning and spatial aggregation. Theor Popul Biol. 2010;77(3):213–218. - PubMed
-
- Anazawa M. Bottom-up derivation of population models for competition involving multiple resources. Theor Popul Biol. 2012;81(2):158–167. - PubMed
-
- Anazawa M. Interspecific competition models derived from competition among individuals. Bull Math Biol. 2012;74(7):1580–1605. - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources

