Ultradonut topology of the nuclear envelope

Abstract

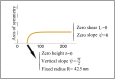
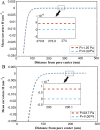
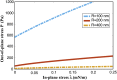
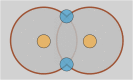
The nuclear envelope is a unique topological structure formed by lipid membranes in eukaryotic cells. Unlike other membrane structures, the nuclear envelope comprises two concentric membrane shells fused at numerous sites with toroid-shaped pores that impart a "geometric" genus on the order of thousands. Despite the intriguing architecture and vital biological functions of the nuclear membranes, how they achieve and maintain such a unique arrangement remains unknown. Here, we used the theory of elasticity and differential geometry to analyze the equilibrium shape and stability of this structure. Our results show that modest in- and out-of-plane stresses present in the membranes not only can define the pore geometry, but also provide a mechanism for destabilizing membranes beyond a critical size and set the stage for the formation of new pores. Our results suggest a mechanism wherein nanoscale buckling instabilities can define the global topology of a nuclear envelope-like structure.

Keywords: buckling instability; lipid membranes; nuclear envelope; topology.

Fig. 1.

Nuclear envelope and the topology. (A) Nuclear envelope with two concentric membrane spheres fused at thousands of sites with toroid-shaped pores. (B) Key geometric parameters that define the nuclear envelope architecture. These include the pore diameter, bilayer separation, and the pore separation. The forces and mechanisms that regulate this unique geometry are not yet understood. (C) Experimental image showing a section of the nuclear envelope with nuclear pores labeled as NP lying in the same observed plane. Other NPs might be out of the plane of observation. [Scale bar, 500 nm (14).] The image shows the uniform bilayer separation and the typical pore separation. Beyond 100 nm, the bilayers essentially become flat and lose the curvature memory associated with the pore region. (D) Shapes exhibiting different genus: sphere has a genus of 0, donut has a genus of 1, and two fused donuts have a genus of 2.

Fig. 2.

Simulated membrane geometry. (A) Because of axisymmetry, only the curve in yellow was simulated. The solid of revolution was obtained by revolving the curve around the vertical axis. (B) The simulated curve subjected to the in-plane and out-of-plane stresses. The arrows indicate the positive directions of the in-plane and out-of-plane stresses. The boundary conditions employed in the simulations are shown in Fig. S1.

Fig. 3.

Impact of in- and out-of plane stresses on membrane geometry. (A) Three-dimensional geometry of a bilayer with $R=500\hspace{0.17em}\text{nm}$, $\lambda =0.15$ mN/m, and $p=1.25\hspace{0.17em}\text{Pa}$. (B) The deflection response of bilayers with different radii R as a function of in-plane stress when subjected to critical out-of-plane stress $p_c$. The bilayers show initial expansion upon λ-reduction. However, they undergo snap-through buckling instability at critical ${\lambda }_c$. (C) Three-dimensional geometry of a buckled bilayer with $R=500\hspace{0.17em}\text{nm}$, $\lambda =-0.0024$ mN/m, and $p=1.25\hspace{0.17em}\text{Pa}$. (D) Two-dimensional geometry of an expanding bilayer for P = 0. The red curve is for λ = −0.04 mN/m and the blue curve is for λ = −0.06 mN/m. (E) Two-dimensional geometry of the buckled bilayer for P = 1.25 Pa. The red curve is for λ = 0.0005 mN/m and the blue curve is for λ = −0.0024 mN/m.

Fig. S1.

Prescribed boundary conditions for the simulation of an axisymmetric bilayer.

Fig. S2.

Deflection response due to a reduction in the in-plane stress for (A) a 200-nm-radius bilayer at $p=0$; (B) a 200-nm-radius bilayer at $p=63.1\hspace{0.17em}\text{Pa}$; (C) a 300-nm-radius bilayer at $p=0$; (D) a 300-nm-radius bilayer at $p=10.6\hspace{0.17em}\text{Pa}$; (E) a 400-nm-radius bilayer at $p=0$; and (F) a 400-nm-radius bilayer at $p=3.02\hspace{0.17em}\text{Pa}$.

Fig. S3.

Mean curvature variation along the bilayer for (A) a 500-nm-radius patch size and 0.15-mN/m in-plane stress and (B) a 250-nm-radius patch size and 0.15-mN/m in-plane stress.

Fig. S4.

Deflection response of the bilayers with different radii for a nominal $p=5\hspace{0.17em}\text{Pa}$. Bilayers with radii equal and smaller to 300 nm continue to expand out and do not undergo instability. In contrast, bilayers with 400- and 500-nm radii undergo buckling instability. Also note that the bilayer with R = 500 nm undergoes instability at tensile in-plane stress. This shows the high vulnerability of larger bilayers ($\sim$500-nm radius) to in-plane stress reduction.

Fig. S5.

Magnitude of out-of-plane stress (p) required to bend the membrane to fusion point for a range of positive in-plane stress values. For every size, a bilayer can undergo inward deformation even in the presence of tensile in-plane stresses due to the applied out-of-plane stress.

Fig. S6.

Three-dimensional geometry of the buckled bilayer. In this scenario we assume both bilayers are buckling toward each other. This does not influence the stresses required to buckle because of the sharp decrease in the bilayer height near the critical point.

Fig. 4.

Ease of buckling depends on the bilayer size. (A) Critical out-of-plane stress ($p_c$) needed to buckle a bilayer inward as a function of the inverse of the bilayer area (text adjacent to the data points shows the corresponding bilayer radius). The critical pressure undergoes a significant increase for $R<200$ nm. (B) Critical in-plane stress (${\lambda }_c$) needed to buckle a bilayer inward as a function of the inverse of the bilayer area (text adjacent to the data points shows the corresponding bilayer radius). The critical stress varies linearly with the inverse of the area. The slope of the curve is ${\lambda }_c\sim -23\kappa /A$ (κ is the bending modulus and A is the area of the simulated bilayer). (C) The deflection response of bilayers with different radii R as a function of in-plane stress when subjected to $p=1.25\hspace{0.17em}\text{Pa}$. Bilayers with $R\le 400$ deform outward, whereas bilayer with $R=500$ buckle inward. The plot reveals the propensity of larger bilayers to undergo instability at minimal in- and out-of-plane stresses.

Fig. S7.

Figure showing the interaction of fusion domains around two neighboring pores (shown in yellow). The blue regions indicate the hot spots at the interaction of two fusion domains. The inner radius of the red annulus indicates the predicted critical length scale that determines the pore separation. The width of the red annulus is controlled by the density of the existing pores. If the density is high, the width is small, and if the density is low, the width is large, leading to a bigger fusion domain where the two membranes meet.