"Threshold-crossing": A Useful Way to Establish the Counterfactual in Clinical Trials?

Abstract

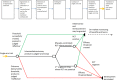
A central question in the assessment of benefit/harm of new treatments is: how does the average outcome on the new treatment (the factual) compare to the average outcome had patients received no treatment or a different treatment known to be effective (the counterfactual)? Randomized controlled trials (RCTs) are the standard for comparing the factual with the counterfactual. Recent developments necessitate and enable a new way of determining the counterfactual for some new medicines. For select situations, we propose a new framework for evidence generation, which we call "threshold-crossing." This framework leverages the wealth of information that is becoming available from completed RCTs and from real world data sources. Relying on formalized procedures, information gleaned from these data is used to estimate the counterfactual, enabling efficacy assessment of new drugs. We propose future (research) activities to enable "threshold-crossing" for carefully selected products and indications in which RCTs are not feasible.

Figure 1

Flow diagram of a threshold crossing trial. The top panel shows the initial, linear sequence of steps, and the bottom panel describes the adaptive follow‐up after completion of the initial single‐arm trial. RCT, randomized controlled trial.

Figure 2

We performed clinical trial simulations to evaluate the operating characteristics of threshold‐crossing trials when frequentist hypothesis tests and corresponding sample size calculations for single‐arm trials are naively applied. To demonstrate the efficacy of a new drug, the most common approach is to conduct parallel group trials to show superiority of the new treatment over control, i.e. testing the null hypothesis $H_0: {\mu }_N\le {\mu }_C$ versus the alternative $H_1: {\mu }_N>{\mu }_C$ at one‐sided significance level of 2.5%, where ${\mu }_N$ and ${\mu }_C$ denote the expected response in the new and control treatment arm, respectively. For the results presented we assume a normally distributed endpoint with σ=1. For example, if such a trial was powered at 80% to detect a standardized effect difference of Δ= $\frac{{\mu }_N-{\mu }_C}{\sigma }$=0.2 between the new and the control treatment, a sample size of around 400 patients per group would be required resulting in a total trial sample size of 800 (red horizontal line in panel a). Alternatively, one may apply a threshold‐crossing single arm trial testing $H_0^t: {\mu }_N\le t$ versus $H_1^t: {\mu }_N>t$ using a one‐sample test at one‐sided level 2.5%, where t is the a‐priori fixed threshold determined from historical controls. What is the impact on the error rates, if one takes a rejection of $H_0^t: {\mu }_N\le t$ naively as a rejection for $H_0: {\mu }_N\le {\mu }_C$? Assume trialists naively use the observed mean estimated from historical controls as threshold t. A conventional sample size calculation for a single arm trial yields a trial sample size of about 200 for a standardized effect of Δ=0.2. Hence, in a best‐case scenario, with no uncertainty on the effect size in the control arm, sample size can be reduced to a quarter relative to a parallel group design. However, due to sampling variability, the observed mean in the controls typically does not coincide with the true population mean ${\mu }_C$ (even assuming ${\mu }_C$ would be identical for historical and concurrent controls). As a consequence, the power to reject $H_0$ decreases with decreasing sample size in the historical controls due to increasing variability of the historical estimate (blue line panel b). In addition, the type I error rate to erroneously reject $H_0$ can be substantially inflated for small sample sizes of historical controls (blue line panel c). In contrast, both the type I error rate and the power (if the true standardized effect is indeed Δ=0.2) of the parallel group design with concurrent controls do not depend on the historical data (red line in panels b and c). The uncertainty due to the sampling variability when estimating the historical response could be addressed by a more cautious choice of the threshold t, e.g., taking the upper boundary of a two‐sided 95%‐confidence interval for µ_C computed from historical controls. A conventional sample size calculation for a single arm trial accounting for a higher threshold (i.e., adjusting the standardized effect 0.2 size by the half width of the confidence interval) yields a sample size of about 400 (=half of that for the parallel group design), if about 1000 historical controls were available (see black line in panel a). The more historical data are available, the lower the resulting sample size for the new threshold‐crossing trial. Assuming ${\mu }_C$ is identical for historical and concurrent controls, the type I error rate is controlled (black line panel c), however a loss of power is observed if the historical control data base is small (black line panel b). Furthermore, if ${\mu }_C$ differs between historical and concurrent controls, e.g., the mean response under control treatment is increasing over time, there might be an inflation of the type I error rate with the thresholding single‐arm design (panel d black line), but not for the traditional two arm parallel group design (with concurrent controls). To address such biases, one may apply even more conservative (larger) thresholds t, for example by adding a percentage of the assumed standardized effect to the upper boundary of the historical 95% confidence interval (e.g., adding 0.1Δ, 0.2Δ, and 0.3Δ for yellow, green and gray lines in panels). This comes at the cost of larger sample sizes (see panel a), but by using sufficiently conservative (large) thresholds, an inflation of the type I error rate to erroneously reject $H_0$ can be avoided (see green and gray line in panel d). For simplicity we have assumed that all historical controls come from one data source, e.g., a single clinical trial or a registry. If several sources are to be used, one has to account for between trial variability as well, e.g., by replacing the sample mean estimate of µ_C by a meta‐analytic estimate of µ_C obtained from a fixed or random effects meta‐analysis of historical controls. panel a: Sample sizes, power and type I error rate are given for a parallel‐group design and single‐arm threshold designs applying different thresholds. The sample size of the historical controls is shown on the x‐axis. The operating characteristics of the designs shown in panels b, c, and d are based on the sample sizes shown in panel a (that depend on the size of historical controls and assumed thresholds).