The Selective Maintenance of Allelic Variation Under Generalized Dominance

Abstract

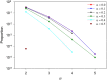
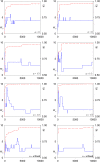
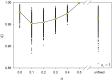
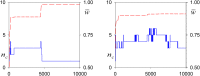
Simple models of viability selection acting on variation at a single diploid locus only maintain multiple alleles for very restricted sets of fitnesses. Most of these models assume that fitnesses are independent, even if the genotypes share alleles. Here, we extend this result to a model with generalized dominance interactions, in which fitnesses are strongly affected by what we call the "primary effects" of the genotype's component alleles, so that genotypes with shared alleles have correlated fitnesses. Nevertheless, in keeping with previously reported results, we also show that such fitness sets are easily constructed over time if recurrent mutation is occurring simultaneously. We find that such models maintain less variation over time than do (previous) models with independently sampled fitnesses, especially when the effects of genetic drift are taken into account. We also show that there is a weak tendency for greater weighting of primary effects to evolve over time.

Keywords: mathematical model; multiple alleles; natural selection; polymorphism; selection theory.

Figure 1

Parameter/state space maintaining all n alleles. The red line with filled circles shows the potential for polymorphism with α = 0 (as in Lewontin et al. 1978); α = 0.1: dark blue line with squares; α = 0.2: black line with upright triangles. α = 0.3: green line with diamonds. α = 0.4: light blue line with upside-down triangles. α = 0.5: purple circle.

Figure 2

Representative simulations of the construction of polymorphism maintained by viability selection with allelic effects for α = 0.0, ⅓, ½, and for when it was unfixed. Upper (dashed red line) shows the mean fitness of the population, $\overline{w},$ and the lower (solid blue) line shows the numbers of common alleles over generations 0–10,000.

Figure 3

Bar chart of the number of common alleles at Generation 10⁴ in 2000 replicate simulations of the constructionist simulations of viability selection for α = 0 (as in Marks and Spencer 1991), ⅓, ½ and for when α is unfixed. The respective means are shown by the vertical colored arrows.

Figure 4

Scatter plot of the values of $\overline{w}$ at Generation 10⁴ in simulations in which the final number of common alleles, n_c, was 3, for different values of α. Also shown for the sake of comparison is the spread when α was unfixed. Mean values are plotted as yellow circles.

Figure 5

Histogram of the α values generated for homozygotes (α_i,i, left) and heterozygotes (α_i,j, right) of common alleles at Generation 10⁴ from 2000 runs of the constructionist simulation when α was randomly sampled and free to evolve.

Figure 6

Histograms of $I={{\displaystyle \sum _{i=1}^{n_c}\left(p_i-\frac{1}{n_c}\right)}}^2,$ a measure of centrality of common allele frequencies at Generation 10⁴ in the constructionist approach with allelic effects at α = ⅓ (i.e., equal parts X_i, X_j, and Y_i,j) for simulations that had three common alleles at Generation 10⁴ (black dashed lines). Also shown (solid blue line) is the distribution expected if allele frequencies were random, values generated using the broken-stick approach.

Figure 7

Representative simulations of the construction of polymorphism maintained by viability selection with allelic effects (α = ⅓) and drift (N = 10⁴). Upper (dashed red line) shows the mean fitness of the population, $\overline{w},$ and the lower (solid blue) line shows the numbers of common alleles over generations 0–10,000.

Figure 8

Bar chart comparing the final number of common alleles for α = ½, ⅓ for 2000 replicates of the constructionist simulation incorporating genetic drift, with population size, N = 10⁴, 10⁵, and ∞ (i.e., no drift), colored blue, gray and black respectively.

Figure 9

Average $\overline{w}$ at Generation 10⁴ for N = 10⁴, 10⁵, and ∞ (blue, black and red lines, respectively) against values of α. Only data from simulations with n_c = 3 were used.

Figure 10

Histograms of $I={{\displaystyle \sum _{i=1}^{n_c}\left(p_i-\frac{1}{n_c}\right)}}^2,$ a measure of centrality of common allele frequencies at Generation 10⁴ in the constructionist approach with the allelic effects weighted at α = ⅓ for N = 10⁴, 10⁵, and ∞ (blue dashed lines, red dashed lines, blue dotted line). Also shown is the distribution expected if allele frequencies were random, values generated using the broken-stick approach (solid black line).