Effect of Axial Stretch on Lumen Collapse of Arteries

Abstract

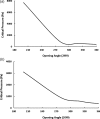
The stability of the arteries under in vivo pressure and axial tension loads is essential to normal arterial function, and lumen collapse due to buckling can hinder the blood flow. The objective of this study was to develop the lumen buckling equation for nonlinear anisotropic thick-walled arteries to determine the effect of axial tension. The theoretical equation was developed using exponential Fung strain function, and the effects of axial tension and residual stress on the critical buckling pressure were illustrated for porcine coronary arteries. The buckling behavior was also simulated using finite-element analysis. Our results demonstrated that lumen collapse of arteries could occur when the transmural pressure is negative and exceeded a critical value. This value depends upon the axial stretch ratio and material properties of the arterial wall. Axial tensions show a biphasic effect on the critical buckling pressure. The lumen aspect ratio of arteries increases nonlinearly with increasing external pressure beyond the critical value as the lumen collapses. These results enhance our understanding of artery lumen collapse behavior.

Fig. 1

Schematic of a sector of an artery cross section deforming from circular configuration into buckled configuration. When the artery is under an internal pressure (p_i) and an external pressure (p_e), the inner radius and the outer radius are (r_i) and (r_e), respectively. The deformation is based on the plane assumption of curved beam bending, with (r_m) and (${\rho }_m$) denoting the radius of the neutral axis in the circular and buckled states.

Fig. 2

Comparison of the critical buckling pressures obtained by theoretical model equations (theory) and by FEA simulations (FEA) for five porcine coronary arteries (artery 1–5 in Table 1) at various axial stretch ratios

Fig. 3

Change of the critical buckling pressure with opening angle (2 ${\Theta }_0$): (a) artery no. 1 at an axial stretch ratio = 1.1 and (b) artery no. 2 at an axial stretch ratio = 1.5

Fig. 4

Deformation of an artery under increasing external pressure. (a) Cross-sectional views from left to right: under no load, axially stretched, under a small pressure without buckling, slightly buckled, and postbuckling. (b) Aspect ratio of the lumen (major to minor axis ratio) plotted with pressure for different axial stretch ratios. (c) Lumen area plotted with pressure for different axial stretch ratios.