A 2D virtual reality system for visual goal-driven navigation in zebrafish larvae
- PMID: 27659496
- PMCID: PMC5034285
- DOI: 10.1038/srep34015
A 2D virtual reality system for visual goal-driven navigation in zebrafish larvae
Abstract
Animals continuously rely on sensory feedback to adjust motor commands. In order to study the role of visual feedback in goal-driven navigation, we developed a 2D visual virtual reality system for zebrafish larvae. The visual feedback can be set to be similar to what the animal experiences in natural conditions. Alternatively, modification of the visual feedback can be used to study how the brain adapts to perturbations. For this purpose, we first generated a library of free-swimming behaviors from which we learned the relationship between the trajectory of the larva and the shape of its tail. Then, we used this technique to infer the intended displacements of head-fixed larvae, and updated the visual environment accordingly. Under these conditions, larvae were capable of aligning and swimming in the direction of a whole-field moving stimulus and produced the fine changes in orientation and position required to capture virtual prey. We demonstrate the sensitivity of larvae to visual feedback by updating the visual world in real-time or only at the end of the discrete swimming episodes. This visual feedback perturbation caused impaired performance of prey-capture behavior, suggesting that larvae rely on continuous visual feedback during swimming.
Figures

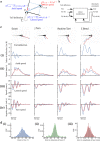
 and the present and past values of the tail deflection:
and the present and past values of the tail deflection:  . See Materials and Methods for details. (c) Examples of four different types of movements showing the true path of the larva (in blue) and that predicted (in red). (i) Tail deflection corresponding to different categories of movement. (ii) The axial speed. (iii) The lateral speed. (iv) Yaw angle. For each case, the observed kinematic parameter is in red, and the predicted in blue. (d) Distribution of the errors between the predicted position and orientation, and those observed, for: (i) change in head orientation; (ii) direction of movement; (iii) amplitude of the tail bout. The results presented in (c) and (d) were taken from the test dataset.
. See Materials and Methods for details. (c) Examples of four different types of movements showing the true path of the larva (in blue) and that predicted (in red). (i) Tail deflection corresponding to different categories of movement. (ii) The axial speed. (iii) The lateral speed. (iv) Yaw angle. For each case, the observed kinematic parameter is in red, and the predicted in blue. (d) Distribution of the errors between the predicted position and orientation, and those observed, for: (i) change in head orientation; (ii) direction of movement; (iii) amplitude of the tail bout. The results presented in (c) and (d) were taken from the test dataset.
 ) as a function of time during the trial. The time scale is common to (c), (d) and (e). (f) Histogram of latency as a function of the initial orientation of the grating, error bar indicates s.e.m. (g) Average of |θ|, for successive bouts, error bar indicates s.e.m. (h) Average percentage of trajectories aligned with the moving stimulus (
) as a function of time during the trial. The time scale is common to (c), (d) and (e). (f) Histogram of latency as a function of the initial orientation of the grating, error bar indicates s.e.m. (g) Average of |θ|, for successive bouts, error bar indicates s.e.m. (h) Average percentage of trajectories aligned with the moving stimulus ( ), at the beginning and at the end of the trials, for each larva. The average is shown in red.
), at the beginning and at the end of the trials, for each larva. The average is shown in red.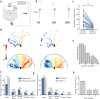

References
-
- Edelman S. The minority report: some common assumptions to reconsider in the modelling of the brain and behaviour. Journal of Experimental & Theoretical Artificial Intelligence 28, 1–26 (2015).
-
- Chen X. & Engert F. Navigational strategies underlying phototaxis in larval zebrafish. Front. Syst. Neurosci. 8 (2014). http://dx.doi.org/10.3389/fnsys.2014.00039. - DOI - PMC - PubMed
-
- Mischiati M. et al. Internal models direct dragonfly interception steering. Nature 517, 333–338 (2015). - PubMed
LinkOut - more resources
Full Text Sources
Other Literature Sources
Molecular Biology Databases

