Quantum decoherence dynamics of divacancy spins in silicon carbide

Abstract

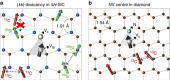
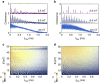
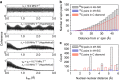
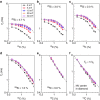
Long coherence times are key to the performance of quantum bits (qubits). Here, we experimentally and theoretically show that the Hahn-echo coherence time of electron spins associated with divacancy defects in 4H-SiC reaches 1.3 ms, one of the longest Hahn-echo coherence times of an electron spin in a naturally isotopic crystal. Using a first-principles microscopic quantum-bath model, we find that two factors determine the unusually robust coherence. First, in the presence of moderate magnetic fields (30 mT and above), the ²⁹Si and ¹³C paramagnetic nuclear spin baths are decoupled. In addition, because SiC is a binary crystal, homo-nuclear spin pairs are both diluted and forbidden from forming strongly coupled, nearest-neighbour spin pairs. Longer neighbour distances result in fewer nuclear spin flip-flops, a less fluctuating intra-crystalline magnetic environment, and thus a longer coherence time. Our results point to polyatomic crystals as promising hosts for coherent qubits in the solid state.

Figure 1. Defect spin qubits in nuclear spin baths.

(a) A depiction of the neutral (kk)-divacancy defect complex in 4H–SiC, in which a carbon vacancy (V_C, white sphere) at a quasi-cubic site (k) is paired with a silicon vacancy (V_Si, white sphere) formed at the nearest neighbouring (k) site. (b) A depiction of the negatively charged NV centre in diamond, which consists of a carbon vacancy (V_C, white sphere) paired with a substitutional nitrogen impurity (N, green sphere). Both defects have the same C_3v symmetry (denoted by a grey pyramid) and spin-1 (black arrow) triplet ground state mainly derived from the surrounding carbon sp³ dangling bonds. While the NV center spin is coupled to a homogeneous ¹³C nuclear spin bath (1.1%, I_C=1/2 represented with red arrows), the divacancy spin interacts with a heterogeneous nuclear spin bath of ¹³C and ²⁹Si (4.7%, I_Si=1/2 represented with green arrows).

Figure 2. Hahn-echo coherence of the divacancy ensemble in 4H–SiC.

(a,b) Experimental (a) and theoretical (b) Hahn-echo coherence of the m_s=+1 to m_s=0 ground-state spin transition of the divacancy ensemble with the c-axis-oriented magnetic field (B) at three different values. The experimental data was taken at T=20 K. (c,d) Experimental (c) and theoretical (d) Hahn-echo coherence of the spin transition from a and b, respectively, as a continuous function of free evolution time (t_free) and B. The early loss of coherence near 47 mT in c corresponds to the spin triplet's ground-state level anti-crossing (GSLAC).

Figure 3. Analysis of the divacancy coherence.

(a) Experimental Hahn-echo coherence time (T₂) of the divacancy spin ensemble as a function of magnetic field (B) (filled circles) compared with theoretical T₂ of the divacancy (empty circles) and theoretical T₂ of the NV centre in diamond (empty diamonds). The divacancy T₂ rises significantly, up to ∼20 mT, and is then roughly constant, except for a dip at 47 mT, corresponding to the ground-state level anti-crossing (GSLAC). (b) A direct comparison between the theoretical (red curve) and experimental (black curve) Hahn-echo coherence of the divacancy spin ensemble at two different magnetic fields of 17.5 mT (up) and 12.5 mT (down). (c,d) Experimental (c) and theoretical (d) FFT power spectrum of the m_s=+1 to m_s=0 ground-state spin coherence data of the divacancy from Fig. 2c,d, respectively. The frequency axis (x axis) is normalized to B, so that the nuclear precession frequencies appear as vertical lines. Harmonics of these frequencies can also be seen both in theory and experiment. After 7 mT, the FFT intensities diminish as B is increased. The hyperbolic features denoted by dotted arrows correspond to weak hyperfine interactions.

Figure 4. Effective decoupling of the ¹³C and ²⁹Si spin baths in 4H–SiC.

(a) The theoretical Hahn-echo coherence function of the divacancy ensemble at B=30 mT, calculated by only including the single- and heterogeneous pair-correlation contributions as defined in equation (3) and by varying the gyromagnetic ratio of ²⁹Si (γ_Si) as a theoretical parameter while that of ¹³C (γ_C) is fixed at its experimental value. (b) The average number of homogeneous nuclear spin pairs whose lengths are <6 Å, as a function of distance from the divacancy qubit in 4H–SiC and from the NV centre in diamond. The centre-of-mass of a nuclear spin pair is used to measure the distance from the qubit. (c) The spatial distribution of homogeneous nuclear spin pairs in 4H–SiC and in diamond. The shortest homogeneous nuclear spin pair in diamond is 1.54 Å, corresponding to the C–C bond length, while that of the homogeneous nuclear spin pair in 4H–SiC is 3.07 Å, which is the second nearest neighbouring Si–Si or C–C distances.

Figure 5. Divacancy coherence time in isotopically purified 4H–SiC.

(a–f) Theoretical Hahn-echo coherence times (T₂) of the divacancy ensemble in 4H–SiC (a–e) and the NV centre in diamond (f) as a function of ¹³C isotope concentration with a fixed ²⁹Si concentration at 4.7% (a), 3.0% (b), 2.0% (c), 1.0% (d) and 0.0% (e) at five different magnetic fields. The black dashed line is the scaling law in equation (6) in the main text.