A touch of sleep: biophysical model of contact-mediated dormancy of archaea by viruses
- PMID: 27683365
- PMCID: PMC5046894
- DOI: 10.1098/rspb.2016.1037
A touch of sleep: biophysical model of contact-mediated dormancy of archaea by viruses
Abstract
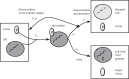
The canonical view of the interactions between viruses and their microbial hosts presumes that changes in host and virus fate requires the initiation of infection of a host by a virus. Infection may lead to the death of the host cell and release of viruses, to the elimination of the viral genome through cellular defence mechanisms or the integration of the viral genome with the host as a chromosomal or extrachromosomal element. Here, we revisit this canonical view, inspired by recent experimental findings in which the majority of target host cells can be induced into a dormant state when exposed to either active or deactivated viruses, even when viruses are present at low relative titre. We propose that both the qualitative phenomena and the quantitative timescales of dormancy induction are consistent with the hypothesis that cellular physiology can be altered by contact on the surface of host cells rather than strictly by infection In order to test this hypothesis, we develop and study a biophysical model of contact-mediated dynamics involving virus particles and target cells. We show how virus particles can catalyse cellular transformations among many cells, even if they ultimately infect only one (or none). We also find that population-scale dormancy is robust to variation in the representation of model dynamics, including cell growth, death and recovery.
Keywords: dormancy; microbes; nonlinear dynamics; viruses.
© 2016 The Author(s).
Figures

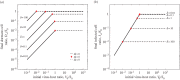

 . The solid line demarcates the boundary between ratios that exceed one (upper-left portion) and those that are less than one (remainder). (a) Population dormancy enhancement as a function of the probability of infection given contact, q, and the probability of dormancy-initiation given reversal of contact, p. Here, S0 = 2.5 × 108 cells ml−1 and V0 = S0/100. (b) Population dormancy enhancement as a function of the initial virus–host ratio, V0/S0, and the cell fate ratio, δ ≈ p/q. Key point: the number of cells that enter dormancy per virus can be much greater than 1, even if the initial virus–host ratio is much smaller than 1.
. The solid line demarcates the boundary between ratios that exceed one (upper-left portion) and those that are less than one (remainder). (a) Population dormancy enhancement as a function of the probability of infection given contact, q, and the probability of dormancy-initiation given reversal of contact, p. Here, S0 = 2.5 × 108 cells ml−1 and V0 = S0/100. (b) Population dormancy enhancement as a function of the initial virus–host ratio, V0/S0, and the cell fate ratio, δ ≈ p/q. Key point: the number of cells that enter dormancy per virus can be much greater than 1, even if the initial virus–host ratio is much smaller than 1.
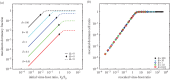
 is plotted as a function of V0/S0 for different values of δ. In each case, the expected domains of behaviour from the asymptotic model are denoted in terms of Ω. (b) Same data as in (a), but plotted with the re-scaled variables
is plotted as a function of V0/S0 for different values of δ. In each case, the expected domains of behaviour from the asymptotic model are denoted in terms of Ω. (b) Same data as in (a), but plotted with the re-scaled variables  versus
versus  , where
, where  ,
,  and
and  . Note that for purposes of visualizing the collapse, only a fraction of simulation results are displayed—all results correspond to the same collapse curve. Here, the parameters of the dynamic simulations are S0 = 2 × 108, ϕ = 2 × 10−9, μ = 1/24, γ = 1/72, d = 1/12, r = 0.23, K = 9 × 108, all in units of hours and ml.
. Note that for purposes of visualizing the collapse, only a fraction of simulation results are displayed—all results correspond to the same collapse curve. Here, the parameters of the dynamic simulations are S0 = 2 × 108, ϕ = 2 × 10−9, μ = 1/24, γ = 1/72, d = 1/12, r = 0.23, K = 9 × 108, all in units of hours and ml.References
LinkOut - more resources
Full Text Sources
Other Literature Sources

