Material gain engineering in GeSn/Ge quantum wells integrated with an Si platform

Abstract

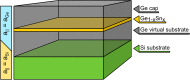
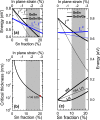
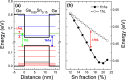
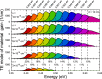
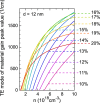
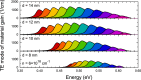
It is shown that compressively strained Ge_1-xSn_x/Ge quantum wells (QWs) grown on a Ge substrate with 0.1 ≤ x ≤ 0.2 and width of 8 nm ≤ d ≤ 14 nm are a very promising gain medium for lasers integrated with an Si platform. Such QWs are type-I QWs with a direct bandgap and positive transverse electric mode of material gain, i.e. the modal gain. The electronic band structure near the center of Brillouin zone has been calculated for various Ge_1-xSn_x/Ge QWs with use of the 8-band kp Hamiltonian. To calculate the material gain for these QWs, occupation of the L valley in Ge barriers has been taken into account. It is clearly shown that this occupation has a lot of influence on the material gain in the QWs with low Sn concentrations (Sn < 15%) and is less important for QWs with larger Sn concentration (Sn > 15%). However, for QWs with Sn > 20% the critical thickness of a GeSn layer deposited on a Ge substrate starts to play an important role. Reduction in the QW width shifts up the ground electron subband in the QW and increases occupation of the L valley in the barriers instead of the Γ valley in the QW region.

Figure 1

A scheme of a Ge_1−xSn_x/Ge QW deposited on a virtual Ge substrate. The QW is in the region where the in-plane lattice constant .

Figure 2

The direct (black lines) and indirect bandgap (blue lines) in unstrained Ge_1−xSn_x (thin lines) and coherently strained Ge_1−xSn_x on Ge (thick lines). (b) Critical thickness of Ge_1−xSn_x layer deposited on Ge substrate. (c) The HH/LH band and conduction band at the Γ and L point in unstrained Ge_1−xSn_x (thin lines) and coherently strained Ge_1−xSn_x on Ge (thick lines).

Figure 3

(a) Electron, heavy hole (black lines) and light hole (grey line) potentials for the 12 nm wide Ge_0.85Sn_0.15/Ge QW together with the electron (blue lines) and hole (red lines) confined states energies and the L valley minimum energy in Ge barriers (green line). (b) The energy of the 1 h1e transition in QW (black circles) and the energy difference 1 hL between the first electron level in QW and L valley in Ge barriers (open circles) obtained for Ge_1−xSn_x/Ge QWs of various Sn concentrations and the width corresponding to the critical thickness at a given Sn concentration.

Figure 4

The electronic band structures along the [100] direction for 8, 10, 12 and 14 nm wide Ge_0.8sSn_0.1s/Ge QWs.

Figure 5

Material TE gain for 12 nm wide QWs with 20%, 15%, 10% Sn contents. There is TE gain calculated with the influence of the L valley (solid lines) and without it (dashed lines).

Figure 6

TE mode of the material gain for 12 nm wide Ge_1−xSn_x/Ge QWs with various Sn concentrations and carrier densities n. Vertical dashed lines show the energy of the fundamental QW transition for each QW.

Figure 7

TE mode of the material gain at the peak position obtained for various Sn concentrations for 12 nm wide Ge_1−xSn_x/Ge QWs with various Sn concentrations.

Figure 8

TE mode of the material gain for Ge_1−xSn_x/Ge QWs with various widths and Sn concentrations.

Figure 9

The peak energy (a) and value (b) obtained for Ge_1−xSn_x/Ge QWs with various widths and Sn concentrations.