Contextuality without nonlocality in a superconducting quantum system

Abstract

Classical realism demands that system properties exist independently of whether they are measured, while noncontextuality demands that the results of measurements do not depend on what other measurements are performed in conjunction with them. The Bell-Kochen-Specker theorem states that noncontextual realism cannot reproduce the measurement statistics of a single three-level quantum system (qutrit). Noncontextual realistic models may thus be tested using a single qutrit without relying on the notion of quantum entanglement in contrast to Bell inequality tests. It is challenging to refute such models experimentally, since imperfections may introduce loopholes that enable a realist interpretation. Here we use a superconducting qutrit with deterministic, binary-outcome readouts to violate a noncontextuality inequality while addressing the detection, individual-existence and compatibility loopholes. This evidence of state-dependent contextuality also demonstrates the fitness of superconducting quantum circuits for fault-tolerant quantum computation in surface-code architectures, currently the most promising route to scalable quantum computing.

Figure 1. KCBS pentagram.

The qutrit eigenstates are |i〉 with i=0, 1 and 2. One can construct five qutrit states |l_i〉 corresponding to five dichotomic observables A_i=2|l_i〉〈l_i|−1. States connected by edges of the pentagram are orthogonal, assuming compatibility of the associated observables. Each pair of compatible measurements forms a context, and each observable is included in two different contexts. The states of the pentagram are chosen to provide maximum contradiction with noncontextual HV models.

Figure 2. System and measurement set-up.

(a) Simplified diagram of the measurement set-up (see Methods for details). (b) The energy level diagram of a qutrit coupled to a microwave cavity when the dispersive shifts of the cavity frequency are identical for the first and second excited states of the qutrit. The scheme realizes the binary-outcome projective measurement of the qutrit on its ground state M_|0〉. (c) Transmission through the readout cavity with the qutrit in different basis states. After state preparation, a square microwave pulse with a frequency close to the resonant frequency of the cavity is applied for several microseconds. The plot indicates the normalized amplitude of measured transmitted signal integrated over 2 μs. 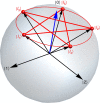The dispersive shifts for and are close to identical, not allowing the measurement to distinguish between the two states.

Figure 3. Measurement potocol.

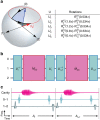
(a) Unitary transformations of the qutrit ground state to the KCBS states. Each U_i can be decomposed into one or two rotations , where ϕ is a rotation of angle about the axis in the qutrit subspace spanned by {|i〉, |i+1〉}. The rightmost pulse in a product is applied first in time. The trajectory of the state under transformation U₄ is shown as an example. (b) The measurement protocol includes two sequential projecting measurements M_|0〉 onto the ground state with unitary transformations before and after each measurement. The unitaries rotate the measurement axis into one of the states of the KCBS pentagram. (c) The actual experimental sequence for each pair of measurements. Measurement of the M_|0〉 observable is implemented with a cavity probe signal and the qutrit rotations are constructed with microwave pulses applied at the qutrit transition frequencies.