Not spreading in reverse: The dewetting of a liquid film into a single drop

Abstract

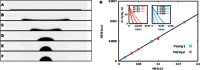
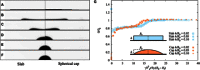
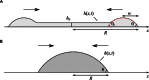
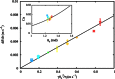
Wetting and dewetting are both fundamental modes of motion of liquids on solid surfaces. They are critically important for processes in biology, chemistry, and engineering, such as drying, coating, and lubrication. However, recent progress in wetting, which has led to new fields such as superhydrophobicity and liquid marbles, has not been matched by dewetting. A significant problem has been the inability to study the model system of a uniform film dewetting from a nonwetting surface to a single macroscopic droplet-a barrier that does not exist for the reverse wetting process of a droplet spreading into a film. We report the dewetting of a dielectrophoresis-induced film into a single equilibrium droplet. The emergent picture of the full dewetting dynamics is of an initial regime, where a liquid rim recedes at constant speed and constant dynamic contact angle, followed by a relatively short exponential relaxation of a spherical cap shape. This sharply contrasts with the reverse wetting process, where a spreading droplet follows a smooth sequence of spherical cap shapes. Complementary numerical simulations and a hydrodynamic model reveal a local dewetting mechanism driven by the equilibrium contact angle, where contact line slip dominates the dewetting dynamics. Our conclusions can be used to understand a wide variety of processes involving liquid dewetting, such as drop rebound, condensation, and evaporation. In overcoming the barrier to studying single film-to-droplet dewetting, our results provide new approaches to fluid manipulation and uses of dewetting, such as inducing films of prescribed initial shapes and slip-controlled liquid retraction.

Keywords: Dewetting; contact-line dynamics; dielectrowetting; slip.

Fig. 1. Experimental imaging of the dewetting of a liquid droplet from a smooth solid surface.

(A) A liquid droplet (TMPTGE; Ω = 1.45 μl, μ = 180 mPa s, γ = 43 mN m⁻¹, T = 22°C, θ_e = 70°) is forced to wet a circular Teflon patch using a dielectrowetting setup. The resulting pancake-shaped liquid film, which corresponds to the initial configuration of the experiment, has a radius R₀ = 2.5 mm. At time t = 0 ms, the dielectrowetting voltage is removed. The dewetting dynamics that follows is tracked by recording the instantaneous film radius, R(t), and the apparent contact angle averaged between the left and right film edges, θ(t). Scale bars, 2 mm. (B and C) At intermediate times, an annular rim forms close to the contact line. The rim is visible from both the top and side views of the film. (D and E) At long times, the rim merges and the film relaxes to a spherical cap shape. (F) Equilibrium state of the droplet, where the radius and contact angle reach constant values, R_f and θ_e. (G and H) Representative curves for the base radius and apparent contact angle. The formation of the rim correlates with a linear decrease in the radius and a plateau in the contact angle. The merging of the rim into a spherical cap gives way to a relaxation stage where the radius and contact angle relax to their final equilibrium values.

Fig. 2. Base radius and apparent angle as a function of time during the dewetting of liquid films.

(A) At intermediate times, the base radius decreases linearly in time, with a dewetting speed that increases with increasing temperature and decreasing volume. (B) The apparent contact angle, θ, is normalized using the equilibrium contact angle, θ_e. The linear dewetting regime, where the speed of the contact line is constant, corresponds to the first plateau. At longer times, there is a crossover to a second plateau, corresponding to the equilibrium state of the drop. The data collapse to a single master curve upon rescaling time by the relaxation time of the rim, τ_rim. The solid line corresponds to the theoretical prediction for the first plateau (see text).

Fig. 3. Lattice Boltzmann simulations of a dewetting film.

(A to F) Instantaneous liquid profiles relaxing from an initial film configuration of aspect ratio h₀/R₀ = 0.02 on a surface where the equilibrium contact angle is θ_e = 70°. In agreement with experiments, the droplet forms a rim (B and C), which eventually merges to form a spherical cap (D and F). (G) The speed of the dewetting rim increases with increasing surface tension and decreasing viscosity (insets). a.u., arbitrary units. Simulation data collapse onto the same scaling curve dR/dt ~ γ/μ.

Fig. 4. Lattice Boltzmann simulations of dewetting films of different initial shapes.

(A to F) Instantaneous liquid profiles relaxing from slab (left) and spherical cap (right) initial configurations. In both cases, the aspect ratio of the initial liquid shape is set to h₀/R₀ = 0.02, and the final equilibrium contact angle is θ_e = 70°. (G) Apparent contact angle as a function of time for different initial aspect ratios of slab and spherical cap–shaped films. The time axis is rescaled by the time scale τ_rim = 9μ(R₀ − R_f)/γθ_e³. The good collapse of the data shows that the rim speed scales with the capillary speed, U_Ca = γθ_e³/9μ, and that the duration of the linear dewetting regime scales with the amplitude of the lateral distortion, R₀ − R_f.

Fig. 5. The two dynamic dewetting regimes of a liquid film.

(A) Schematic shape of the cross-sectional profile of a dewetting film. The cross section of the rim corresponds to two independent structures of width w, connected by a thin film of thickness h₀. The shape of the rim is described by the apparent contact angles θ and θ_f. (B) Schematic of the quasi-equilibrium shape of a dewetting droplet.

Fig. 6. Scaling of the interface speed in the linear regime of a dewetting film.

Speed of the receding rim as a function of the capillary speed U_Ca = γθ_e³/9μ. The solid line is a visual guide. The inset shows a direct comparison of the experimental data (symbols) with the hydrodynamic theory (solid line). Error bars correspond to 1 SD of the sample. Experimental parameters for each symbol are summarized in Table 1.

Fig. 7. Exponential approach to equilibrium of a dewetting droplet.

(A) Difference between the equilibrium and apparent contact angles as a function of time. The solid line corresponds to a fitted exponential function. (B) Scaling of the relaxation time in the exponential regime. The inverse relaxation time is compared to the theoretical prediction. Error bars correspond to 1 SD of the sample. Experimental parameters for each symbol are summarized in Table 1.

Fig. 8. Teflon-coated IDEs.

A circular electrode patch is defined from two interdigitated coplanar metal (Ti/Au) stripe arrays. The electrodes are covered by an insulating SU8 layer (1 μm), which is overcoated with a thin oleophobic layer of Teflon. The resulting pattern has a circular envelope 5 mm in diameter.