A Tutorial on Hunting Statistical Significance by Chasing N

Abstract

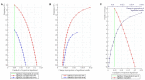
There is increasing concern about the replicability of studies in psychology and cognitive neuroscience. Hidden data dredging (also called p-hacking) is a major contributor to this crisis because it substantially increases Type I error resulting in a much larger proportion of false positive findings than the usually expected 5%. In order to build better intuition to avoid, detect and criticize some typical problems, here I systematically illustrate the large impact of some easy to implement and so, perhaps frequent data dredging techniques on boosting false positive findings. I illustrate several forms of two special cases of data dredging. First, researchers may violate the data collection stopping rules of null hypothesis significance testing by repeatedly checking for statistical significance with various numbers of participants. Second, researchers may group participants post hoc along potential but unplanned independent grouping variables. The first approach 'hacks' the number of participants in studies, the second approach 'hacks' the number of variables in the analysis. I demonstrate the high amount of false positive findings generated by these techniques with data from true null distributions. I also illustrate that it is extremely easy to introduce strong bias into data by very mild selection and re-testing. Similar, usually undocumented data dredging steps can easily lead to having 20-50%, or more false positives.

Keywords: N-hacking; Type I error; bias and data dredging; false positive error; null hypothesis significance testing (NHST); p-hacking; replication crisis.

FIGURE 1

The computation of family-wise error rate. Let’s assume that the null hypothesis is true and we run two independent significance tests with α = 0.05. There are four possible outcomes: (A) The probability that none of the tests can reject the null is 0.95 × 0.95. (B) The probability that the first test does not reject the null but the second does reject it is 0.95 × 0.05. (C) The probability that the first test rejects the null but the second test does not reject it is 0.05 × 0.95. (D) The probability that both tests reject the null is 0.05 × 0.05. The family-wise Type I error rate is the probability that at least one of the tests rejects the null. This is the probability of the complement of (A). That is, the summed probability of all other possible outcomes besides (A). Put more technically, the complement of (A) is the probability of the union of (B–D): 0.0475 + 0.0475 + 0.0025 = 0.0975. Because (A–D) represent all possible outcomes their probabilities sum to 1. Hence, the complement of (A) can also be computed as 1-0.95² = 0.0975.

FIGURE 2

Illustrating how repeated testing of non-independent data sets can lead to the accumulation of false positive Type I errors. The boxes stand for statistical tests run on true null data samples. The empty boxes denote tests with non-significant results. The filled boxes denote tests with statistically significant false positive results. First, we run 40 tests with α = 0.05 and 5% of them (two tests) will come up statistically significant (Run 1). Second, we slightly change the data sets and re-run the tests (Run 2). While again 5% of tests will come up statistically significant, these will not necessarily be the same two data sets as before. A similar phenomenon happens if we slightly change the data again and re-run the tests (Run 3). In the example, the consequence of repeated testing of altered data is that the total Type I error rate in terms of the 40 data sets will be 10% rather than 5%.

FIGURE 3

Increase in statistically significant results when adding additional participants to samples (A,B) and when randomly swapping participants for new ones (C). (A) The figure shows the proportion of false positive significant results independently for each N (green line) and when considered cumulatively up to a particular N (red and blue lines). (B) The rate of increase in statistically significant test outcomes represented in Panel A from a particular N to N+1. (C) Increase in statistically significant results when swapping one randomly chosen participant in the sample for another one. The number of swaps is represented on the Y-axis (0–14 swaps). The green line shows the proportion of statistically significant results independently for each test run. The red line shows the proportion of statistically significant results cumulatively for each test run. The blue line shows the rate of increase in statistically significant results from one swap to the next.

FIGURE 4

Removing the least fitting participants from the sample without replacing them. (A) The proportion of statistically significant findings independently for various numbers of participants (‘N’ on the vertical axis). The black line indicates the proportion of statistically significant findings when testing the original N number of participants. The other lines indicate the proportion of statistically significant findings when removing 1, 2, or 3 participants with the most negative data points from the sample. (B) Illustrates how the mean of sample means changes when removing 1, 2, or 3 participants with the most negative data points from the samples.

FIGURE 5

Increase in statistically significant results when introducing very mild bias and re-testing. (A) The proportion of statistically significant findings independently (green line) and cumulatively (red line) for various swaps. (B) The rate of increase in the proportion of statistically significant findings from one swap to the next. (C) The change introduced into the sample mean by the biasing process is illustrated by plotting the 95% credible interval for the sample means (assessed from the simulation).

FIGURE 6

Using ad hoc grouping variables along weakly or non-correlated variables. (A) Scatterplot for two variables (V1 and V2) with r = 0.05. Groups are defined by V2. The group means on V2 and V1 are indicated by the arrows. (B) Scatterplot for two variables with r = 0.05. (C) The proportion of statistically significant results in correlations and t-tests for various sample sizes. (D) The proportion of statistically significant results when using multiple independent (grouping) variables. See explanation in text.