Estimating infectious disease transmission distances using the overall distribution of cases

Abstract

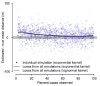
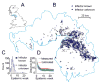
The average spatial distance between transmission-linked cases is a fundamental property of infectious disease dispersal. However, the distance between a case and their infector is rarely measurable. Contact-tracing investigations are resource intensive or even impossible, particularly when only a subset of cases are detected. Here, we developed an approach that uses onset dates, the generation time distribution and location information to estimate the mean transmission distance. We tested our method using outbreak simulations. We then applied it to the 2001 foot-and-mouth outbreak in Cumbria, UK, and compared our results to contact-tracing activities. In simulations with a true mean distance of 106m, the average mean distance estimated was 109m when cases were fully observed (95% range of 71-142). Estimates remained consistent with the true mean distance when only five percent of cases were observed, (average estimate of 128m, 95% range 87-165). Estimates were robust to spatial heterogeneity in the underlying population. We estimated that both the mean and the standard deviation of the transmission distance during the 2001 foot-and-mouth outbreak was 8.9km (95% CI: 8.4km-9.7km). Contact-tracing activities found similar values of 6.3km (5.2km-7.4km) and 11.2km (9.5km-12.8km), respectively. We were also able to capture the drop in mean transmission distance over the course of the outbreak. Our approach is applicable across diseases, robust to under-reporting and can inform interventions and surveillance.

Keywords: Epidemiology; Foot-and-mouth disease; Infectious disease; Outbreaks; Transmission distance.

Figure 1

(A) Example transmission tree with (B) the cumulative distribution function for pairs of cases separated by different numbers of transmission events assuming a constant exponentially distributed transmission kernel with a mean of 100m.

Figure 2

Example calculation of the weights from the Wallinga-Teunis matrix. Assume five cases occur over three days as set out in (A) and we know the generation time distribution (B) so that two thirds of sequential infections are a day apart and one third are two days apart. We can build a Wallinga-Teunis matrix (C) that sets out for each case the probability that a case occurring at each time point was its infector. The columns of the matrix have been normalized so that they add to one. (D) Sets out all possible pathways connecting a case at time 2 with a case at time 3, with the associated number of transmission events (θ) for that chain and the probability of that chain calculated from the Wallinga-Teunis matrix (chains with zero probability such as 4-5-2 have been excluded). (E) sets out the average probability for each θ from (D), which represents the weights used in the calculation of the transmission kernel.

Figure 3

Transmission kernels with different means and standard deviations can produce point patterns with the same mean squared dispersal distance (ER²) and therefore are not distinguishable from each other in the presented approach. (A) Combinations of values with the same ER². (B) Cumulative distribution function of transmission kernels with exponential distribution with μ_k = σ_k =100m (red line in (B, C) and red dot in (A)), uniform distribution between 0 and 246m (green), gamma distribution with μ_k =80m and σ_k =117m (purple), Gaussian distribution with μ_k =140m and σ_k=20m (orange) and log-normal distribution with μ_k =200m and σ_k =500m (grey). Kernels with equivalent ER² in (A) generated points that had indistinguishable cumulative distribution functions after ten generations, whereas the kernel with an inconsistent ER² (in grey) had a different cumulative distribution function.

Figure 4

Estimates of mean transmission distance from simulated transmission chains where only a subset of cases are observed. The blue dots represent estimates from individual simulations with an exponential distributed transmission kernel. The lines represent loess curves from 2000 simulations.

Figure 5

Outbreak of Foot and Mouth Disease in Cumbria, UK in 2001. (A) Location of Cumbria and Dumfriesshire in the UK. (B) Location of cases. (C) Epidemic curve by week. (D) Measured mean transmission distance from contact tracing activities (green) and estimated through our approach (red) for all cases up to each epidemic week with 95% confidence intervals.

Figure 6

(A) Estimate of the mean transmission distance for foot-and-mouth disease in Cumbria in 2001 compared to estimates from contact tracing activities. (B) Weibull distributions with equivalent ER² from Equation 3 (black line in panel A).