Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2016 Oct 13;16(10):1700.
doi: 10.3390/s16101700.

A Stepped Frequency Sweeping Method for Nonlinearity Measurement of Microresonators

Yumiao Wei  1   2 , Yonggui Dong  3 , Xianxiang Huang  4 , Zhili Zhang  5
Affiliations

A Stepped Frequency Sweeping Method for Nonlinearity Measurement of Microresonators

Yumiao Wei et al. Sensors (Basel). .

Abstract

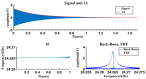
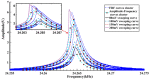
In order to measure the nonlinear features of micromechanical resonators, a free damped oscillation method based on stair-stepped frequency sinusoidal pulse excitation is investigated. In the vicinity of the resonant frequency, a frequency stepping sinusoidal pulse sequence is employed as the excitation signal. A set of free vibration response signals, containing different degrees of nonlinear dynamical characteristics, are obtained. The amplitude-frequency curves of the resonator are acquired from the forced vibration signals. Together with a singular spectrum analysis algorithm, the instantaneous amplitudes and instantaneous frequencies are extracted by a Hilbert transform from the free vibration signals. The calculated Backbone curves, and frequency response function (FRF) curves are distinct and can be used to characterize the nonlinear dynamics of the resonator. Taking a Duffing system as an example, numerical simulations are carried out for free vibration response signals in cases of different signal-to-noise ratios (SNRs). The results show that this method displays better anti-noise performance than FREEVIB. A vibrating ring microgyroscope is experimentally tested. The obtained Backbone and FRF curves agree with those obtained by the traditional frequency sweeping method. As a test technique, the proposed method can also be used to for experimentally testing the dynamic characteristics of other types of micromechanical resonators.

Keywords: Backbone curve; Hilbert transform; MEMS resonators; nonlinear features; singular spectrum analysis.

PubMed Disclaimer

Conflict of interest statement

The authors declare no conflict of interest.

Figures

Figure 1
Figure 1
Typical response of the simulated Duffing system.
Figure 2
Figure 2
System response signals and amplitude-frequency curves corresponding to different excitation: (a) System response signals; (b) Amplitude-frequency curves.
Figure 3
Figure 3
Typical free vibration signal.
Figure 4
Figure 4
Results corresponding to different SNRs obtained by the FREEVIB method: (a) Instantaneous amplitudes (IAs); (b) Instantaneous frequencies (IFs); (c) Backbone and FRF curves.
Figure 5
Figure 5
Results corresponding to different SNRs obtained by the proposed method: (a) Instantaneous amplitudes (IAs); (b) Instantaneous frequencies (IFs); (c) Backbone and FRF curves.
Figure 6
Figure 6
Comparison of the simulation results.
Figure 7
Figure 7
Amplitude-frequency response of the driving mode.
Figure 8
Figure 8
Experimental testing system.
Figure 9
Figure 9
Response of the tested gyroscope under different excitation voltages: (a) Measured response signals; (b) Amplitude-frequency curves.
Figure 10
Figure 10
Free vibration signals of the largest response segments in Figure 9: (a) 50 mV; (b) 75 mV; (c) 100 mV; (d) 125 mV; (e) 150 mV; (f) 200 mV.
Figure 10
Figure 10
Free vibration signals of the largest response segments in Figure 9: (a) 50 mV; (b) 75 mV; (c) 100 mV; (d) 125 mV; (e) 150 mV; (f) 200 mV.
Figure 11
Figure 11
Calculated results for response signals of Figure 10c.
Figure 12
Figure 12
Backbone curves cluster and FRF curves cluster.
Figure 13
Figure 13
Frequency response curves obtained by frequency sweeping: (a) Amplitude-frequency curves; (b) Phase-frequency curves.
Figure 14
Figure 14
Comparison between the Backbone curves cluster and frequency sweeping measurement results.
Figure 15
Figure 15
Contrast between FRF curves cluster, Amplitude-frequency curves cluster and frequency sweeping results.
See this image and copyright information in PMC

References

    1. Tatar E., Mukherjee T., Fedder G.K. Nonlinearity tuning and its effects on the performance of a MEMS gyroscope; Proceedings of the 18th International Conference on Solid-State Sensors, Actuators and Microsystems (TRANSDUCERS); Anchorage, AK, USA. 21–25 June 2015; pp. 1133–1136.
    1. Villanueva L.G., Karabalin R.B., Matheny M.H., Chi D., Sader J.E., Roukes M.L. Nonlinearity in nanomechanical cantilevers. Phys. Rev. B. 2013;87:024304. doi: 10.1103/PhysRevB.87.024304. - DOI
    1. Mestrom R.M.C., Fey R.H.B., Phan K.L., Nijmeijer H. Simulations and experiments of hardening and softening resonances in a clamped–clamped beam MEMS resonator. Sens. Actuators A. 2010;162:225–234. doi: 10.1016/j.sna.2010.04.020. - DOI
    1. Mestrom R.M.C., Fey R.H.B., Van Beek J.T.M., Phan K.L., Nijmeijer H. Modelling the dynamics of a MEMS resonator: simulations and experiments. Sens. Actuators A. 2008;142:306–315. doi: 10.1016/j.sna.2007.04.025. - DOI
    1. Nitzan S.H., Zega V., Li M., Ahn C.H., Corigliano A., Kenny T.W., Horsley D.A. Self-induced parametric amplification arising from nonlinear elastic coupling in a micromechanical resonating disk gyroscope. Sci. Rep. 2015;5:9036. doi: 10.1038/srep09036. - DOI - PMC - PubMed

LinkOut - more resources