False discovery rates: a new deal
- PMID: 27756721
- PMCID: PMC5379932
- DOI: 10.1093/biostatistics/kxw041
False discovery rates: a new deal
Abstract
We introduce a new Empirical Bayes approach for large-scale hypothesis testing, including estimating false discovery rates (FDRs), and effect sizes. This approach has two key differences from existing approaches to FDR analysis. First, it assumes that the distribution of the actual (unobserved) effects is unimodal, with a mode at 0. This "unimodal assumption" (UA), although natural in many contexts, is not usually incorporated into standard FDR analysis, and we demonstrate how incorporating it brings many benefits. Specifically, the UA facilitates efficient and robust computation-estimating the unimodal distribution involves solving a simple convex optimization problem-and enables more accurate inferences provided that it holds. Second, the method takes as its input two numbers for each test (an effect size estimate and corresponding standard error), rather than the one number usually used ($p$ value or $z$ score). When available, using two numbers instead of one helps account for variation in measurement precision across tests. It also facilitates estimation of effects, and unlike standard FDR methods, our approach provides interval estimates (credible regions) for each effect in addition to measures of significance. To provide a bridge between interval estimates and significance measures, we introduce the term "local false sign rate" to refer to the probability of getting the sign of an effect wrong and argue that it is a superior measure of significance than the local FDR because it is both more generally applicable and can be more robustly estimated. Our methods are implemented in an R package ashr available from http://github.com/stephens999/ashr.
Keywords: Empirical Bayes; False discovery rates; Multiple testing; Shrinkage; Unimodal.
© The Author 2016. Published by Oxford University Press.
Figures

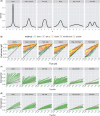
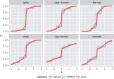
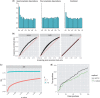
Similar articles
-
Empirical Bayes screening of many p-values with applications to microarray studies.Bioinformatics. 2005 May 1;21(9):1987-94. doi: 10.1093/bioinformatics/bti301. Epub 2005 Feb 2. Bioinformatics. 2005. PMID: 15691856
-
Resampling-based empirical Bayes multiple testing procedures for controlling generalized tail probability and expected value error rates: focus on the false discovery rate and simulation study.Biom J. 2008 Oct;50(5):716-44. doi: 10.1002/bimj.200710473. Biom J. 2008. PMID: 18932138 Free PMC article.
-
fdrtool: a versatile R package for estimating local and tail area-based false discovery rates.Bioinformatics. 2008 Jun 15;24(12):1461-2. doi: 10.1093/bioinformatics/btn209. Epub 2008 Apr 25. Bioinformatics. 2008. PMID: 18441000
-
Simple estimators of false discovery rates given as few as one or two p-values without strong parametric assumptions.Stat Appl Genet Mol Biol. 2013 Aug;12(4):529-43. doi: 10.1515/sagmb-2013-0003. Stat Appl Genet Mol Biol. 2013. PMID: 23798617
-
An investigation of the false discovery rate and the misinterpretation of p-values.R Soc Open Sci. 2014 Nov 19;1(3):140216. doi: 10.1098/rsos.140216. eCollection 2014 Nov. R Soc Open Sci. 2014. PMID: 26064558 Free PMC article. Review.
Cited by
-
"All-In-One" Genetic Tool Assessing Endometrial Receptivity for Personalized Screening of Female Sex Steroid Hormones.Front Cell Dev Biol. 2021 Feb 15;9:624053. doi: 10.3389/fcell.2021.624053. eCollection 2021. Front Cell Dev Biol. 2021. PMID: 33659249 Free PMC article.
-
Tetracycline Antibiotics Induce Host-Dependent Disease Tolerance to Infection.Immunity. 2021 Jan 12;54(1):53-67.e7. doi: 10.1016/j.immuni.2020.09.011. Epub 2020 Oct 14. Immunity. 2021. PMID: 33058782 Free PMC article.
-
Comprehensive alpha, beta, and delta cell transcriptomics reveal an association of cellular aging with MHC class I upregulation.Mol Metab. 2024 Sep;87:101990. doi: 10.1016/j.molmet.2024.101990. Epub 2024 Jul 14. Mol Metab. 2024. PMID: 39009220 Free PMC article.
-
Feeder-free generation and characterization of endocardial and cardiac valve cells from human pluripotent stem cells.iScience. 2023 Nov 30;27(1):108599. doi: 10.1016/j.isci.2023.108599. eCollection 2024 Jan 19. iScience. 2023. PMID: 38170020 Free PMC article.
-
Fine mapping spatiotemporal mechanisms of genetic variants underlying cardiac traits and disease.Nat Commun. 2023 Feb 28;14(1):1132. doi: 10.1038/s41467-023-36638-2. Nat Commun. 2023. PMID: 36854752 Free PMC article.
References
-
- Benjamini Y. and Hochberg Y. (1995). Controlling the false discovery rate: a practical and powerful approach to multiple testing. Journal of the Royal Statistical Society. Series B (Methodological) 57, 289–300.
-
- Benjamini Y. and Yekutieli D. (2005). False discovery rate--adjusted multiple confidence intervals for selected parameters. Journal of the American Statistical Association 100, 71–81.
-
- Boyd S. and Vandenberghe L. (2004). Convex Optimization. Cambridge, UK: Cambridge University Press.
-
- Carvalho C. M. Polson N. G. and Scott J. G. (2010). The horseshoe estimator for sparse signals. Biometrika 97, asq017.
-
- Cordy C. B. and Thomas D. R. (1997). Deconvolution of a distribution function. Journal of the American Statistical Association 92, 1459–1465.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

