Population Density Modulates Drug Inhibition and Gives Rise to Potential Bistability of Treatment Outcomes for Bacterial Infections
- PMID: 27764095
- PMCID: PMC5072716
- DOI: 10.1371/journal.pcbi.1005098
Population Density Modulates Drug Inhibition and Gives Rise to Potential Bistability of Treatment Outcomes for Bacterial Infections
Abstract
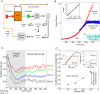
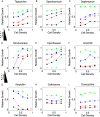
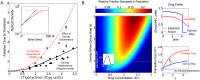
The inoculum effect (IE) is an increase in the minimum inhibitory concentration (MIC) of an antibiotic as a function of the initial size of a microbial population. The IE has been observed in a wide range of bacteria, implying that antibiotic efficacy may depend on population density. Such density dependence could have dramatic effects on bacterial population dynamics and potential treatment strategies, but explicit measures of per capita growth as a function of density are generally not available. Instead, the IE measures MIC as a function of initial population size, and population density changes by many orders of magnitude on the timescale of the experiment. Therefore, the functional relationship between population density and antibiotic inhibition is generally not known, leaving many questions about the impact of the IE on different treatment strategies unanswered. To address these questions, here we directly measured real-time per capita growth of Enterococcus faecalis populations exposed to antibiotic at fixed population densities using multiplexed computer-automated culture devices. We show that density-dependent growth inhibition is pervasive for commonly used antibiotics, with some drugs showing increased inhibition and others decreased inhibition at high densities. For several drugs, the density dependence is mediated by changes in extracellular pH, a community-level phenomenon not previously linked with the IE. Using a simple mathematical model, we demonstrate how this density dependence can modulate population dynamics in constant drug environments. Then, we illustrate how time-dependent dosing strategies can mitigate the negative effects of density-dependence. Finally, we show that these density effects lead to bistable treatment outcomes for a wide range of antibiotic concentrations in a pharmacological model of antibiotic treatment. As a result, infections exceeding a critical density often survive otherwise effective treatments.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures


References
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical
Research Materials

