More reliable inference for the dissimilarity index of segregation

Abstract

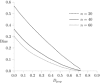
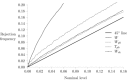
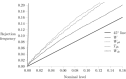
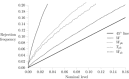
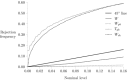
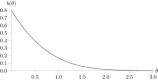
The most widely used measure of segregation is the so-called dissimilarity index. It is now well understood that this measure also reflects randomness in the allocation of individuals to units (i.e. it measures deviations from evenness, not deviations from randomness). This leads to potentially large values of the segregation index when unit sizes and/or minority proportions are small, even if there is no underlying systematic segregation. Our response to this is to produce adjustments to the index, based on an underlying statistical model. We specify the assignment problem in a very general way, with differences in conditional assignment probabilities underlying the resulting segregation. From this, we derive a likelihood ratio test for the presence of any systematic segregation, and bias adjustments to the dissimilarity index. We further develop the asymptotic distribution theory for testing hypotheses concerning the magnitude of the segregation index and show that the use of bootstrap methods can improve the size and power properties of test procedures considerably. We illustrate these methods by comparing dissimilarity indices across school districts in England to measure social segregation.

Keywords: Bootstrap methods; Dissimilarity index; Hypothesis testing; Segregation.

Figure 1

Bias $E\left[D\right]-D_{\mathrm{pop}}$, $J=4$, $p=0.1$, equal expected unit sizes.

Figure 2

P‐value plot, $H_0:D_{\mathrm{pop}}=0.292$, $E\left[n_j\right]=30$, $J=50$, $p=0.30$.

Figure 3

P‐value plot, $H_0:D_{\mathrm{pop}}=0.292$, $E\left[n_j\right]=20$, $J=50$, $p=0.10$.

Figure 4

P‐value plot, $H_0:D_{\mathrm{pop},1}=D_{\mathrm{pop},1}$, size properties.

Figure 5

P‐value plot, $H_0:D_{\mathrm{pop},1}=D_{\mathrm{pop},1}$, power properties.

Figure A.1

Bias function $b\left({\theta }_j\right)$.