Simulating the exchange of Majorana zero modes with a photonic system
- PMID: 27779181
- PMCID: PMC5093330
- DOI: 10.1038/ncomms13194
Simulating the exchange of Majorana zero modes with a photonic system
Abstract
The realization of Majorana zero modes is in the centre of intense theoretical and experimental investigations. Unfortunately, their exchange that can reveal their exotic statistics needs manipulations that are still beyond our experimental capabilities. Here we take an alternative approach. Through the Jordan-Wigner transformation, the Kitaev's chain supporting two Majorana zero modes is mapped to the spin-1/2 chain. We experimentally simulated the spin system and its evolution with a photonic quantum simulator. This allows us to probe the geometric phase, which corresponds to the exchange of two Majorana zero modes positioned at the ends of a three-site chain. Finally, we demonstrate the immunity of quantum information encoded in the Majorana zero modes against local errors through the simulator. Our photonic simulator opens the way for the efficient realization and manipulation of Majorana zero modes in complex architectures.
Figures

 ,
,  ,
,  and
and  , respectively. The letters A and B in each pane represent the corresponding isolated Majorana zero modes. The mapping between the Kitaev chain model (KCM) and the transverse-field Ising model (TFIM) through the JW transformation is shown in e. m3f and k3s are bases of the ground-state spaces defined in the KCM and TFIM (m and k=0 or 1), respectively.
, respectively. The letters A and B in each pane represent the corresponding isolated Majorana zero modes. The mapping between the Kitaev chain model (KCM) and the transverse-field Ising model (TFIM) through the JW transformation is shown in e. m3f and k3s are bases of the ground-state spaces defined in the KCM and TFIM (m and k=0 or 1), respectively.
 . The polarization of single photons is rotated using HWPs and quarter-wave plate (QWPs), and the spatial modes are separated by BDs, each with a beam displacement of either 3.0 mm (BD30) or 6.0 mm (BD60). The state preparation is illustrated in the pane labelled Pre. The basis rotations BR1, BR2 and BR3 are used to express the input states in terms of the eigenstates of H1, H2 and H0, respectively. The dissipative evolutions DE0, DE1 and DE2 drive the input states to the ground states of H0, H1 and H2, respectively. Some of the detailed basis representations of the spatial modes are given in the right column. The solid magenta rings represent the preserved optical modes and the dashed magenta rings represent the discarded optical modes. The states indicated near the optical modes represent the corresponding preserved basis in the eight-dimensional space. Two types of measurements are performed, that is, TM and FM. Beam splitters (BSs) are used to send the photons to different measurement instruments. H, V, R and D represent the horizontal polarization, vertical polarization, right-hand circular polarization and diagonal polarization, respectively. Finally, photons are detected using single-photon detectors (SPDs).
. The polarization of single photons is rotated using HWPs and quarter-wave plate (QWPs), and the spatial modes are separated by BDs, each with a beam displacement of either 3.0 mm (BD30) or 6.0 mm (BD60). The state preparation is illustrated in the pane labelled Pre. The basis rotations BR1, BR2 and BR3 are used to express the input states in terms of the eigenstates of H1, H2 and H0, respectively. The dissipative evolutions DE0, DE1 and DE2 drive the input states to the ground states of H0, H1 and H2, respectively. Some of the detailed basis representations of the spatial modes are given in the right column. The solid magenta rings represent the preserved optical modes and the dashed magenta rings represent the discarded optical modes. The states indicated near the optical modes represent the corresponding preserved basis in the eight-dimensional space. Two types of measurements are performed, that is, TM and FM. Beam splitters (BSs) are used to send the photons to different measurement instruments. H, V, R and D represent the horizontal polarization, vertical polarization, right-hand circular polarization and diagonal polarization, respectively. Finally, photons are detected using single-photon detectors (SPDs).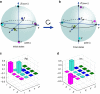
 (−Y direction),
(−Y direction),  (−Z direction),
(−Z direction),  (+X direction, |03s〉),
(+X direction, |03s〉),  (+Y direction) and
(+Y direction) and  (−X direction, |13s〉), respectively. Owing to the experimental errors, the coloured dots (experimental results) are slightly separated from the corresponding black dots. The final states are shown to be rotated along the X axis by π/2 from the initial states. (c) Real (Re) and (d) imaginary (Im) parts of the exchange operator in the basis of {I(identity), X(σx), Y(σy), Z(σz)}, with a fidelity of 94.13±0.04%.
(−X direction, |13s〉), respectively. Owing to the experimental errors, the coloured dots (experimental results) are slightly separated from the corresponding black dots. The final states are shown to be rotated along the X axis by π/2 from the initial states. (c) Real (Re) and (d) imaginary (Im) parts of the exchange operator in the basis of {I(identity), X(σx), Y(σy), Z(σz)}, with a fidelity of 94.13±0.04%.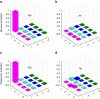
References
-
- Wilczek F. & Zee A. Appearance of gauge structure in simple dynamical systems. Phys. Rev. Lett. 52, 2111–2114 (1984).
-
- Nayak C. S., Stern S. H., Freedman A. & Sarma D. S. Non-abelian anyons and topological quantum computation. Rev. Mod. Phys. 80, 1083–1159 (2008).
-
- Fu L. & Kane C. Superconducting proximity effect and Majorana fermions at the surface of a topological insulator. Phys. Rev. Lett. 100, 096407 (2008). - PubMed
-
- Sau J. D. L., Tewar R. M. & Sarma D. S. Generic new platform for topological quantum computation using semiconductor heterostructures. Phys. Rev. Lett. 104, 040502 (2010). - PubMed
-
- Kitaev A. Y. Unpaired Majorana fermions in quantum wires. Phys. Usp. 44, 131–136 (2001).
Publication types
LinkOut - more resources
Full Text Sources
Other Literature Sources

