Heart Valve Biomechanics and Underlying Mechanobiology
- PMID: 27783858
- PMCID: PMC5537387
- DOI: 10.1002/cphy.c150048
Heart Valve Biomechanics and Underlying Mechanobiology
Abstract
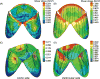
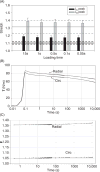
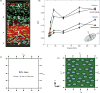
Heart valves control unidirectional blood flow within the heart during the cardiac cycle. They have a remarkable ability to withstand the demanding mechanical environment of the heart, achieving lifetime durability by processes involving the ongoing remodeling of the extracellular matrix. The focus of this review is on heart valve functional physiology, with insights into the link between disease-induced alterations in valve geometry, tissue stress, and the subsequent cell mechanobiological responses and tissue remodeling. We begin with an overview of the fundamentals of heart valve physiology and the characteristics and functions of valve interstitial cells (VICs). We then provide an overview of current experimental and computational approaches that connect VIC mechanobiological response to organ- and tissue-level deformations and improve our understanding of the underlying functional physiology of heart valves. We conclude with a summary of future trends and offer an outlook for the future of heart valve mechanobiology, specifically, multiscale modeling approaches, and the potential directions and possible challenges of research development. © 2016 American Physiological Society. Compr Physiol 6:1743-1780, 2016.
Copyright © 2016 John Wiley & Sons, Inc.
Figures

















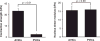
References
-
- Abrams J. The aortic valve by Mano Thubrikar Crc Press, Inc., Boca Raton (1990) 221 pages, illustrated, $97.50 ISBN: 0–8493–4771–8. Clin Cardiol. 1991;14:364a–365.
-
- Accola KD, Scott ML, Thompson PA, Palmer GJ, III, Sand ME, Ebra G. Midterm outcomes using the physio ring in mitral valve reconstruction: Experience in 492 patients. Ann Thorac Surg. 2005;79:1276–1283. discussion 1276–1283. - PubMed
-
- Adamczyk MM, Vesely I. Characteristics of compressive strains in porcine aortic valves cusps. J Heart Valve Dis. 2002;11:75–83. - PubMed
-
- Aikawa E, Otto CM. Look more closely at the valve: Imaging calcific aortic valve disease. Circulation. 2012;125:9–11. - PubMed
-
- Aikawa E, Whittaker P, Farber M, Mendelson K, Padera RF, Aikawa M, Schoen FJ. Human semilunar cardiac valve remodeling by activated cells from fetus to adult: Implications for postnatal adaptation, pathology, and tissue engineering. Circulation. 2006;113:1344–1352. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

