Mechanics of human voice production and control

Abstract

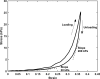
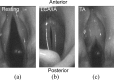
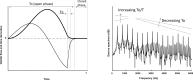
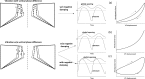
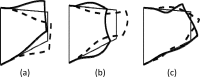
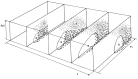
As the primary means of communication, voice plays an important role in daily life. Voice also conveys personal information such as social status, personal traits, and the emotional state of the speaker. Mechanically, voice production involves complex fluid-structure interaction within the glottis and its control by laryngeal muscle activation. An important goal of voice research is to establish a causal theory linking voice physiology and biomechanics to how speakers use and control voice to communicate meaning and personal information. Establishing such a causal theory has important implications for clinical voice management, voice training, and many speech technology applications. This paper provides a review of voice physiology and biomechanics, the physics of vocal fold vibration and sound production, and laryngeal muscular control of the fundamental frequency of voice, vocal intensity, and voice quality. Current efforts to develop mechanical and computational models of voice production are also critically reviewed. Finally, issues and future challenges in developing a causal theory of voice production and perception are discussed.

FIG. 1.

(Color online) (a) Coronal view of the vocal folds and the airway; (b) histological structure of the vocal fold lamina propria in the coronal plane (image provided by Dr. Jennifer Long of UCLA); (c) superior view of the vocal folds, cartilaginous framework, and laryngeal muscles; (d) medial view of the cricoarytenoid joint formed between the arytenoid and cricoid cartilages; (e) posterolateral view of the cricothyroid joint formed by the thyroid and the cricoid cartilages. The arrows in (d) and (e) indicate direction of possible motions of the arytenoid and cricoid cartilages due to LCA and CT muscle activation, respectively.

FIG. 2.

Typical tensile stress-strain curve of the vocal fold along the anterior-posterior direction during loading and unloading at 1 Hz. The slope of the tangent line (dashed lines) to the stress-strain curve quantifies the tangent stiffness. The stress is typically higher during loading than unloading due to the viscous behavior of the vocal folds. The curve was obtained by averaging data over 30 cycles after a 10-cycle preconditioning.

FIG. 3.

Activation of the LCA/IA muscles completely closes the posterior glottis but leaves a small gap in the membranous glottis, whereas TA activation completely closes the anterior glottis but leaves a gap at the posterior glottis. From unpublished stroboscopic recordings from the in vivo canine larynx experiments in Choi et al. (1993).

FIG. 4.

(Color online) Typical glottal flow waveform and its time derivative (left) and their correspondence to the spectral slopes of the low-frequency and high-frequency portions of the voice source spectrum (right).

FIG. 5.

Two energy transfer mechanisms. Top row: the presence of a vertical phase difference leads to different medial surface shapes between glottal opening (dashed lines 5 and 6; upper left panel) and closing (solid lines 2 and 3) when the lower margin of the medial surface crosses the same locations, which leads to higher air pressure during glottal opening than closing and net energy transfer from airflow into vocal folds at the lower margin of the medial surface. Middle row: without a vertical phase difference, vocal fold vibration produces an alternatingly convergent-divergent but identical glottal channel geometry between glottal opening and closing (bottom left panel), thus zero energy transfer (middle row). Bottom row: without a vertical phase difference, air pressure asymmetry can be imposed by a negative damping mechanism.

FIG. 6.

Typical vocal fold eigenmodes exhibiting (a) a dominantly superior-inferior motion, (b) a medial-lateral in-phase motion, and (c) a medial-lateral out-of-phase motion along the medial surface.

FIG. 7.

A typical eigenmode synchronization pattern. The evolution of the first three eigenmodes is shown as a function of the subglottal pressure. As the subglottal pressure increases, the frequencies (top) of the second and third vocal fold eigenmodes gradually approach each other and, at a threshold subglottal pressure, synchronize to the same frequency. At the same time, the growth rate (bottom) of the second mode becomes positive, indicating the coupled airflow-vocal fold system becomes linearly unstable and phonation starts.

FIG. 8.

(Color online) The closed quotient CQ and vertical phase difference VPD as a function of the medial surface thickness, the AP stiffness (G_ap), and the resting glottal angle (α). Reprinted with permission of ASA from Zhang (2016a).

FIG. 9.

A three-dimensional map of normal (N), breathy (B), and rough (R) phonation in the parameter space of the prephonatory glottal area (Ag0), subglottal pressure (Ps), vocal fold stiffness (k). Reprinted with permission of Springer from Isshiki (1989).