Biomolecular interactions modulate macromolecular structure and dynamics in atomistic model of a bacterial cytoplasm
- PMID: 27801646
- PMCID: PMC5089862
- DOI: 10.7554/eLife.19274
Biomolecular interactions modulate macromolecular structure and dynamics in atomistic model of a bacterial cytoplasm
Abstract
Biological macromolecules function in highly crowded cellular environments. The structure and dynamics of proteins and nucleic acids are well characterized in vitro, but in vivo crowding effects remain unclear. Using molecular dynamics simulations of a comprehensive atomistic model cytoplasm we found that protein-protein interactions may destabilize native protein structures, whereas metabolite interactions may induce more compact states due to electrostatic screening. Protein-protein interactions also resulted in significant variations in reduced macromolecular diffusion under crowded conditions, while metabolites exhibited significant two-dimensional surface diffusion and altered protein-ligand binding that may reduce the effective concentration of metabolites and ligands in vivo. Metabolic enzymes showed weak non-specific association in cellular environments attributed to solvation and entropic effects. These effects are expected to have broad implications for the in vivo functioning of biomolecules. This work is a first step towards physically realistic in silico whole-cell models that connect molecular with cellular biology.
Keywords: biophysics; computational biology; crowding effects; diffusion; metabolite dynamics; native state stability; none; quinary interactions; structural biology; systems biology; whole-cell modeling.
Conflict of interest statement
The authors declare that no competing interests exist.
Figures




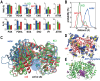




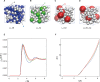






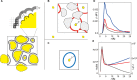
References
-
- Asakura S, Oosawa F. Interaction between particles suspended in solutions of macromolecules. Journal of Polymer Science. 1958;33:183–192. doi: 10.1002/pol.1958.1203312618. - DOI
-
- Banchio AJ, Brady JF. Accelerated stokesian dynamics: Brownian motion. The Journal of Chemical Physics. 2003;118:10323–10332. doi: 10.1063/1.1571819. - DOI
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

