The Protein Cost of Metabolic Fluxes: Prediction from Enzymatic Rate Laws and Cost Minimization

Abstract

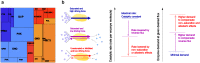
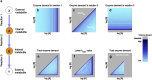
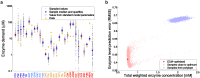
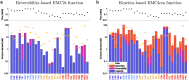
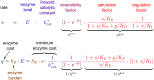
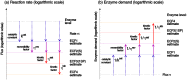
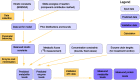
Bacterial growth depends crucially on metabolic fluxes, which are limited by the cell's capacity to maintain metabolic enzymes. The necessary enzyme amount per unit flux is a major determinant of metabolic strategies both in evolution and bioengineering. It depends on enzyme parameters (such as kcat and KM constants), but also on metabolite concentrations. Moreover, similar amounts of different enzymes might incur different costs for the cell, depending on enzyme-specific properties such as protein size and half-life. Here, we developed enzyme cost minimization (ECM), a scalable method for computing enzyme amounts that support a given metabolic flux at a minimal protein cost. The complex interplay of enzyme and metabolite concentrations, e.g. through thermodynamic driving forces and enzyme saturation, would make it hard to solve this optimization problem directly. By treating enzyme cost as a function of metabolite levels, we formulated ECM as a numerically tractable, convex optimization problem. Its tiered approach allows for building models at different levels of detail, depending on the amount of available data. Validating our method with measured metabolite and protein levels in E. coli central metabolism, we found typical prediction fold errors of 4.1 and 2.6, respectively, for the two kinds of data. This result from the cost-optimized metabolic state is significantly better than randomly sampled metabolite profiles, supporting the hypothesis that enzyme cost is important for the fitness of E. coli. ECM can be used to predict enzyme levels and protein cost in natural and engineered pathways, and could be a valuable computational tool to assist metabolic engineering projects. Furthermore, it establishes a direct connection between protein cost and thermodynamics, and provides a physically plausible and computationally tractable way to include enzyme kinetics into constraint-based metabolic models, where kinetics have usually been ignored or oversimplified.

Fig 1. Enzyme cost in metabolism.

(a) Measured enzyme levels in E. coli central metabolism (molecule counts displayed as rectangle areas). Colors correspond to the network graphics in Fig 3. To predict such protein levels, and to explain the differences between enzymes, we start from known metabolic fluxes and assume that these fluxes are realized by a cost-optimal distribution of enzyme levels. (b) Enzyme-specific flux depends on a number of physical factors. Under ideal conditions, an enzyme molecule catalyzes its reaction at a maximal rate given by the enzyme’s forward catalytic constant (top left). The rate is reduced by microscopic reverse fluxes (center left) and by incomplete saturation with substrate (causing waiting times between reaction events) or by allosteric inhibition or incomplete activation (bottom left). With lower catalytic rates (center), realizing the same metabolic flux requires larger amounts of enzyme (right).

Fig 2. Enzyme demand in a metabolic pathway.

(a) Pathway with reversible Michaelis-Menten kinetics (equilibrium constants, catalytic constants, and K_M values are set to values of 1, [A] and [B] denote the variable concentrations of intermediates A and B in mM). The external metabolite levels [X] and [Y] are fixed. Plots (b)-(d) show the enzyme demand of reactions 1, 2, and 3 at given flux v = 1 according to Eq (2). Grey regions represent infeasible metabolite profiles. At the edges of the feasible region (where A and B are close to chemical equilibrium), the thermodynamic driving force goes to zero. Since small forces must be compensated by high enzyme levels, edges of the feasible region are always dark blue. For example, in reaction 1 (panel (b)), enzyme demand increases with the level of A (x-axis) and goes to infinity as the mass-action ratio [A]/[X] approaches the equilibrium constant (where the driving force vanishes). (e) Total enzyme demand, obtained by summing all enzyme levels. The metabolite polytope—the intersection of feasible regions for all reactions—is a triangle, and enzyme demand is a convex function on this triangle. The point of minimum total enzyme demand defines the optimal metabolite levels and optimal enzyme levels. (f) As the k_cat value of the first reaction is lowered by a factor of 5, states close to the triangle edge of reaction 1 become more expensive and the optimum point is shifted away from the edge. (g) The same model with a physiological upper bound on the concentration [A]. The bound defines a new triangle edge. Since this edge is not caused by thermodynamics, it can contain an optimum point, in which driving forces are far from zero and enzyme costs are kept low.

Fig 3. Predicted enzyme levels in E. coli central metabolism.

(a) Network model with pathways marked by colors. Flux magnitudes are represented by the arrows’ thickness. (b) The ratio flux/$k_{\text{cat}}^{+}$ (EMC1) as a predictor for enzyme levels. Points on the dashed line would represent precise predictions. (c) Enzyme levels predicted by the reversibility-based EMC2(S) function. Vertical bars indicate tolerance ranges obtained from a relaxed optimality condition (allowing for a one percent increase in total enzyme cost). (d) Enzyme levels predicted with EMC3 function representing fast substrate or product binding. (e) Enzyme levels predicted with EMC4 function based on the common modular rate law [21]. In all sub-figures (b-e), RMSE is the root mean squared error (in log₁₀-scale) of our predictions compared to the measured enzyme levels, and r stands for the Pearson correlation coefficient. Predictions are based on fluxes from [52], $k_{\text{cat}}^{+}$ and K_M values from BRENDA [40], and compared to protein data from [53]. For metabolite predictions, see Figure E in S1 Text.

Fig 4. Prediction uncertainties and evidence for cost optimality.

(a) Uncertainty of predicted enzyme levels due to uncertain model parameters. A hundred sets of kinetic model parameters were generated by Monte Carlo sampling. Due to the multivariate distribution used for sampling, each parameter set satisfies the Haldane relationships. At the same time, fluxes were sampled according to their experimental error bars (typically around 15% of the measured flux), and the fixed metabolite concentrations were randomly varied in a ± 5% range. The resulting predicted enzyme levels, computed using the EMC4cm score, are shown by small gray dots. Solid blue circles show medians, and error bars show 25% and 75% quantiles; empty red circles show the original ECM4cm prediction, i.e. without sampling. (b) The enzyme levels in E. coli appear to be cost-optimized. We compared the ECM solution (with ECM4cm score) to enzyme profiles obtained from metabolite profiles randomly sampled in the metabolite polytope. The ECM solution (red) or metabolite profiles sampled in a close neighborhood (pink) yield significantly better enzyme predictions (quantified by RMSE, compare Fig 3) than metabolite profiles sampled in the entire polytope (light blue). The total enzyme cost (on x-axis) represents the sum of weighted enzyme concentrations (in mM); the weight of an enzyme is given by its amino chain length, divided by the median chain length of all enzymes considered.

Fig 5. Enzyme demand in central metabolism.

(a) Measured fluxes for all reactions (black dots on top) lead to an enzyme demand (bottom). The enzyme demand, predicted by using the reversibility-based EMC2s cost function, can be split into factors representing enzyme capacity and thermodynamics (see Methods). Bars show predicted enzyme levels in mM for individual enzymes on logarithmic scale. Yellow dots denote measured enzyme levels (in μM). Note that the bars do not represent additive costs, but multiplicative cost terms on logarithmic scale; therefore, the relevant feature of the blue bars is not their absolute lengths, but their differences between enzymes. (b) The kinetics-based EMC4cm cost function includes saturation terms and yields more accurate predictions. Starting from the capacity cost (in blue), the reversibility (purple) and saturation (red) terms increase the enzyme demands and decrease the variability between enzymes (on log-scale). Note that flux data (circles) and protein data (yellow dots) are identical in both plots.

Fig 6. Rate law and enzyme demand of reversible Meichalis-Menten reactions.

For a reaction S ⇌ P with reversible Michaelis-Menten kinetics, a driving force θ = −Δ_rG′/RT, and a prefactor for non-competitive allosteric inhibition, the rate law can be written as with inhibitor concentration x. In the example, with non-competitive allosteric inhibition, the kinetic factor η^kin could even be split into a product η^sat ⋅ η^reg. The first two terms in our example, $E·k_{\text{cat}}^{+}$, represent the maximal velocity (the rate at full substrate-saturation, no backward flux, full allosteric activation), while the following factors decrease this velocity for different reasons: the factor η^rev describes a decrease due to backward fluxes (see Figure A in S1 Text) and the factor η^kin describes a further decrease due to incomplete substrate saturation and allosteric regulation (see Fig 1b). The inverse of all these terms appear in the equation for enzyme demand, q, which is given by the enzyme level multiplied by the burden of that enzyme, h_E.

Fig 7. The conversion between fluxes and enzyme levels, in both directions.

(a) Starting from the logarithmic enzyme level (dashed line on top), we add the terms $log{k}_{\text{cat}}^{+}$, log η^rev, and log η^kin, and obtain better and better approximation of the rate. In the example shown, $k_{\text{cat}}^{+}$ has a numerical value smaller than 1. The more precise approximations (with more terms) yield smaller rates. The EMC4 arrows refer to other possible rate laws with additional terms in the denominator. (b) Enzyme demand is shaped by the same factors (see Eq (5)). Starting from a desired flux (bottom line), the predicted demand increases as more terms are considered.

Fig 8. Data integration in the ECM-based modeling workflow.

After collecting all available kinetic and thermodynamic data and mapping them onto the network model, we use parameter balancing to obtain a consistent, complete set of kinetic constants. For a fully parameterized kinetic model, the metabolite and enzyme levels must be determined. We compute them by enzyme cost minimization with predefined metabolic fluxes (obtained from experiments or computationally). Finally, the predicted values are validated with measured metabolite and protein concentrations.