How numbers mean: Comparing random walk models of numerical cognition varying both encoding processes and underlying quantity representations
- PMID: 27821255
- PMCID: PMC5171212
- DOI: 10.1016/j.cogpsych.2016.10.002
How numbers mean: Comparing random walk models of numerical cognition varying both encoding processes and underlying quantity representations
Abstract
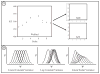
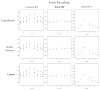
How do people derive meaning from numbers? Here, we instantiate the primary theories of numerical representation in computational models and compare simulated performance to human data. Specifically, we fit simulated data to the distributions for correct and incorrect responses, as well as the pattern of errors made, in a traditional "relative quantity" task. The results reveal that no current theory of numerical representation can adequately account for the data without additional assumptions. However, when we introduce repeated, error-prone sampling of the stimulus (e.g., Cohen, 2009) superior fits are achieved when the underlying representation of integers reflects linear spacing with constant variance. These results provide new insights into (i) the detailed nature of mental numerical representation, and, (ii) general perceptual processes implemented by the human visual system.
Keywords: Numerical architecture; Numerical cognition; Numerical distance; Physical similarity; Random walk; Simulation.
Copyright © 2016 Elsevier Inc. All rights reserved.
Figures
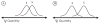




References
-
- Ashby FG. A stochastic version of general recognition theory. Journal of Mathematical Psychology. 2000;44:310–329. http://dx.doi.org/10.1006/JMPS.1998.1249. - DOI - PubMed
-
- Ashby FG, Maddox WT. A response time theory of separability and integrality in speeded classification. Journal of Mathematical Psychology. 1994;38:423–466. http://dx.doi.org/10.1006/jmps.1994.1032. - DOI
-
- Balakrishan JD, Ratcliff R. Testing models of decision making under confidence ratings in classification. Journal of Experimental Psychology: Human Perception and Performance. 1996;22:615–633. http://dx.doi.org/10.1037/0096-1523.22.3.615. - DOI - PubMed
-
- Banks WP, Fum M, Kayra-Stuart F. Semantic congruity effects in comparative judgments of magnitudes of digits. Journal of Experimental Psychology: Human Perception and Performance. 1976;2:435–447. http://dx.doi.org/10.1037/0096-1523.2.3.435. - DOI
-
- Bergstra J, Bengio Y. Random search for hyper-parameter optimization. Journal of Machine Learning Research. 2012;13:281–305.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

