Optimization and Control of Agent-Based Models in Biology: A Perspective

Abstract

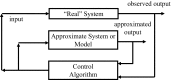
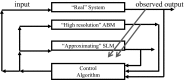
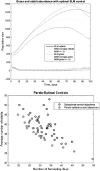
Agent-based models (ABMs) have become an increasingly important mode of inquiry for the life sciences. They are particularly valuable for systems that are not understood well enough to build an equation-based model. These advantages, however, are counterbalanced by the difficulty of analyzing and using ABMs, due to the lack of the type of mathematical tools available for more traditional models, which leaves simulation as the primary approach. As models become large, simulation becomes challenging. This paper proposes a novel approach to two mathematical aspects of ABMs, optimization and control, and it presents a few first steps outlining how one might carry out this approach. Rather than viewing the ABM as a model, it is to be viewed as a surrogate for the actual system. For a given optimization or control problem (which may change over time), the surrogate system is modeled instead, using data from the ABM and a modeling framework for which ready-made mathematical tools exist, such as differential equations, or for which control strategies can explored more easily. Once the optimization problem is solved for the model of the surrogate, it is then lifted to the surrogate and tested. The final step is to lift the optimization solution from the surrogate system to the actual system. This program is illustrated with published work, using two relatively simple ABMs as a demonstration, Sugarscape and a consumer-resource ABM. Specific techniques discussed include dimension reduction and approximation of an ABM by difference equations as well systems of PDEs, related to certain specific control objectives. This demonstration illustrates the very challenging mathematical problems that need to be solved before this approach can be realistically applied to complex and large ABMs, current and future. The paper outlines a research program to address them.

Keywords: Agent-based modeling; Optimal control; Optimization; Systems theory.

Fig. 1

Basic block diagram of a system

Fig. 2

Model-based control block diagram

Fig. 3

(Color Figure Online) Two levels of modeling in a decision and control loop

Fig. 4

(Color Figure Online) Upper panels show the time course of the SLM and ABM, the latter with an average of 100 realizations and +/- 2 standard deviations. The top shows the system with no control applied, and the bottom illustrates a Pareto-optimal control. Third panel shows average number of rabbits versus days of harvesting. The red symbols represent Pareto points, while the black symbols show suboptimal controls

Fig. 5

(Color Figure Online) Time course of grass and rabbit abundance, comparing ABM and SLM. Upper panel compares the models without any control applied, while the lower panel compares the two with the SLM’s optimal control

Fig. 6

(Color Figure Online) Time course of grass and rabbit abundance. Upper panel compares the models without any control applied, while the lower panel compares the two with the SLM’s optimal control