An oscillating tragedy of the commons in replicator dynamics with game-environment feedback

Abstract

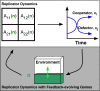
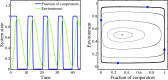
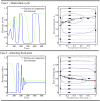
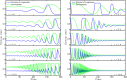
A tragedy of the commons occurs when individuals take actions to maximize their payoffs even as their combined payoff is less than the global maximum had the players coordinated. The originating example is that of overgrazing of common pasture lands. In game-theoretic treatments of this example, there is rarely consideration of how individual behavior subsequently modifies the commons and associated payoffs. Here, we generalize evolutionary game theory by proposing a class of replicator dynamics with feedback-evolving games in which environment-dependent payoffs and strategies coevolve. We initially apply our formulation to a system in which the payoffs favor unilateral defection and cooperation, given replete and depleted environments, respectively. Using this approach, we identify and characterize a class of dynamics: an oscillatory tragedy of the commons in which the system cycles between deplete and replete environmental states and cooperation and defection behavior states. We generalize the approach to consider outcomes given all possible rational choices of individual behavior in the depleted state when defection is favored in the replete state. In so doing, we find that incentivizing cooperation when others defect in the depleted state is necessary to avert the tragedy of the commons. In closing, we propose directions for the study of control and influence in games in which individual actions exert a substantive effect on the environmental state.

Keywords: cooperation; environmental dynamics; evolutionary games; game theory; nonlinear dynamics.

Fig. 1.

Schematic of replicator dynamics in feedback-evolving games. (Top) In replicator dynamics, the payoff matrix A determines frequency-dependent changes in strategies, $x_i$. (Top and Bottom) In replicator dynamics with feedback-evolving games, the frequencies of strategies influences the environment n, which, in term modifies the payoffs, $A\left(n\right)$. The coupled system includes dynamics of both the payoff matrix and the strategies.

Fig. 2.

Persistent oscillations of strategies and the environment. (Left) Time series of the fraction of cooperators x (blue) and the environmental state n (green), correspond to dynamics arising from Eq. 17 with $\mathrm{ϵ}=0.1$, $\theta =2$, and the payoffs $R=3$, $S=0$, $T=5$, and $P=1$. (Right) Phase plane dynamics of $x-n$ system. The arrows denote the direction of dynamics with time. The distinct curves correspond to initial conditions $\left(0.9,0.01\right)$, $\left(0.8,0.15\right)$, $\left(0.7,0.3\right)$, $\left(0.5,0.4\right)$, and $\left(0.4,0.45\right)$. SI Appendix A includes a proof of the existence of a constant of motion associated with these dynamics. The asterisk denotes the predicted neutrally stable fixed point at $\left(1/3,1/2\right)$.

Fig. 3.

Fast–slow dynamics of feedback-evolving games, where x and n are the fast and slow variables, respectively—including critical manifolds and realized dynamics. In both panels, the black lines denote the critical manifolds with solid denoting attractors and dashed denoting repellers. The blue lines and double arrows denote expected fast dynamics in the limit $\mathrm{ϵ}\to 0$. The red circles denote the bifurcation points of the fast subsystem parameterized by n. The single arrows denote expected slow dynamics. The gray curve denotes the realized orbit. In both cases, $\mathrm{ϵ}=0.1$ and $\theta =2$. (Top) Relaxation oscillations converging to a heteroclinic cycle arising due to a saddle-node bifurcation in the fast subsystem parameterized by n in which the critical manifold is a repeller. The payoff matrix $A\left(n\right)$ is that defined in Eq. 21. (Bottom) Relaxation oscillations converging to a fixed point arising due to a saddle-node bifurcation in the fast subsystem parameterized by n in which the critical manifold is an attractor. The payoff matrix $A\left(n\right)$ is that defined in Eq. 23.

Fig. 4.

Invariance of system dynamics given change in the relative speed of strategy and environmental dynamics. The parameter ε is varied from 0.1 to 10 given cases where dynamics are expected to lead to a heteroclinic cycle (Left) and to an interior fixed point (Right). Other parameters are the same as in Fig. 3. Although the transient dynamics differ, the qualitative dynamics remain invariant with respect to changes in ε.

Fig. 5.

Summary of dynamics given all possible combinations of payoffs in the depleted state. The axes correspond to the relative values of $S_0-P_0$ and $R_0-T_0$. There are seven regions identified. The Inset include schematics of dynamics corresponding to each combination of payoff values, where the closed circle denotes a locally stable fixed point. In all cases, we consider a scenario in which the system has a unique Nash equilibrium corresponding to mutual defection in the replete state, $n=1$. SI Appendix D includes detailed analysis and numerical simulations for the bottom right and upper left quadrants.