A MAD-Bayes Algorithm for State-Space Inference and Clustering with Application to Querying Large Collections of ChIP-Seq Data Sets

Abstract

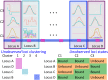
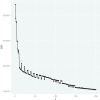
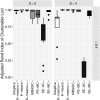
Current analytic approaches for querying large collections of chromatin immunoprecipitation followed by sequencing (ChIP-seq) data from multiple cell types rely on individual analysis of each data set (i.e., peak calling) independently. This approach discards the fact that functional elements are frequently shared among related cell types and leads to overestimation of the extent of divergence between different ChIP-seq samples. Methods geared toward multisample investigations have limited applicability in settings that aim to integrate 100s to 1000s of ChIP-seq data sets for query loci (e.g., thousands of genomic loci with a specific binding site). Recently, Zuo et al. developed a hierarchical framework for state-space matrix inference and clustering, named MBASIC, to enable joint analysis of user-specified loci across multiple ChIP-seq data sets. Although this versatile framework estimates both the underlying state-space (e.g., bound vs. unbound) and also groups loci with similar patterns together, its Expectation-Maximization-based estimation structure hinders its applicability with large number of loci and samples. We address this limitation by developing MAP-based asymptotic derivations from Bayes (MAD-Bayes) framework for MBASIC. This results in a K-means-like optimization algorithm that converges rapidly and hence enables exploring multiple initialization schemes and flexibility in tuning. Comparison with MBASIC indicates that this speed comes at a relatively insignificant loss in estimation accuracy. Although MAD-Bayes MBASIC is specifically designed for the analysis of user-specified loci, it is able to capture overall patterns of histone marks from multiple ChIP-seq data sets similar to those identified by genome-wide segmentation methods such as ChromHMM and Spectacle.

Keywords: ChIP-Seq; MAD-Bayes; small-variance asymptotics; unified state-space inference and clustering.

FIG. 1.

Overview of the MBASIC modeling framework. Curves within each panel depict different replicates under the experimental conditions C1, C2, and C3. Loci A and D are in the same cluster.

FIG. 2.

(a) Run-time comparisons on a 64 bit machine with Intel Xeon 3.0 GHz processor and 64GB of RAM and eight cores. (b) State-space prediction error. (c) Clustering accuracy based on the adjusted Rand index. (d) Clustering assignments of the singletons when

FIG. 3.

(a) Comparison of clusters and state labels between MAD-Bayes, Spectacle, and ChromHMM. (b) Jaccard index between MAD-Bayes clusters and ChromHMM states. (c) Jaccard index between MAD-Bayes clusters and Spectacle states. The diagonal blocks indicate agreement between clusters and states; MAD-Bayes clusters and Spectacle states are ordered according to their overlap with the ChromHMM states. MAD-Bayes, MAP-based asymptotic derivations from Bayes.

Appendix FIG. 1.

A graphical interpretation of the conjugacy between and J. We use the K-means initialization to compute surrogate values for for a large collection of . The value that can yield J clusters in the global solution must satisfy When satisfies this condition, a line with slope passing through on the graph should be tangent to the trace of all values. Although using the surrogate values can lead to the curve connecting the values to be non-convex, making the solution for not hold for some J, we can use a convex approximation to the trace of so that a exists for each J. A simpler approach is to order from largest to smallest and requires the following condition for . . Algorithm 2 essentially applies this idea to select the values. Each J corresponds to a of value that satisfies the conjugacy inequality. The algorithm essentially tries to identify the range of that leads up to number of clusters.

Appendix FIG. 2.

Comparison of the clustering accuracy with the adjusted Rand index by excluding the singleton loci.