A framework for discrete stochastic simulation on 3D moving boundary domains

Abstract

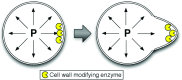
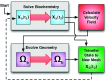
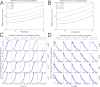
We have developed a method for modeling spatial stochastic biochemical reactions in complex, three-dimensional, and time-dependent domains using the reaction-diffusion master equation formalism. In particular, we look to address the fully coupled problems that arise in systems biology where the shape and mechanical properties of a cell are determined by the state of the biochemistry and vice versa. To validate our method and characterize the error involved, we compare our results for a carefully constructed test problem to those of a microscale implementation. We demonstrate the effectiveness of our method by simulating a model of polarization and shmoo formation during the mating of yeast. The method is generally applicable to problems in systems biology where biochemistry and mechanics are coupled, and spatial stochastic effects are critical.

FIG. 1.

Diagram illustrating the how the yeast mating projection grows, our motivating example. Cell wall modifying enzymes (yellow) are localized to the polarized region of the cell membrane. These enzymes soften the cell wall. The internal turgor pressure pushes on the cell wall, deforming it, and creating the mating projection.

FIG. 2.

Diagram illustrating the process flow of the moving mesh algorithm.

FIG. 3.

Diagram illustrating the particle redistribution process. On each step of the moving mesh simulation, the state of the biochemical system is transferred from the old mesh (left) to the new mesh (right). The x, y, z position of each particle is sampled on the old mesh (uniformly from within the volume of the containing voxel); the particle is assigned to the voxel in the new mesh that is closest to that sampled position. If the species of a particle is restricted to a subdomain (e.g., membrane-bound proteins), then it is moved to the closest voxel in that subdomain.

FIG. 4.

Error in distribution as a function of the size of the time step for a 1D moving domain with an absorbing/desorbing boundary for three different reactive rates (columns) and three different spatial discretizations (rows). Our mesoscopic method was compared with a Brownian dynamics microscopic simulation of ${10}^6$ molecules. We define the error as the Kolmogorov-Smirnov distance between the spatial distributions of unbound particles at the end time (1s). As we can see by comparing the middle three panels to the bottom three panels, the error is similar to N_vox = 20 and N_vox = 50, meaning that the problem is spatially well-resolved already with N_vox = 20, while for N_vox = 5 we can see that the system is not fully resolved for the case of k_a = 50 and k_d = 1.0. As expected, the larger the speed v of the expansion, the larger the error, but as the splitting time step $\mathrm{\Delta }{t}_{\text{split}}$ decreases, so does the error. For v = 0.05, the domain is expanding so slowly that the stochastic error dominates, and no difference is seen as $\mathrm{\Delta }{t}_{\text{split}}$ varies between 0.01 and 0.2.

FIG. 5.

Comparison of our method to theoretical results from the literature. As expected, the error for our method decreases with the velocity of the boundary and the time step. (a) Relative error in 2-norm for a variety of expansion velocities (v) and operator-split time steps for an expanding sphere. (b) Relative error in 2-norm for a variety of contraction velocities (v) and operator-split time steps for a contracting sphere. (c) 95% confidence intervals for three trajectories at a variety of expansion velocities (v) and operator-split time steps (Δt_split) for an expanding sphere, along with the theoretical value (dashed red line). (d) 95% confidence intervals for three trajectories at a variety of contraction velocities (v) and operator-split time steps (Δt_split) for a contracting sphere, along with the theoretical value (dashed red line).

FIG. 6.

(a) Time series of heatmaps showing the number of membrane-bound molecules on the surface of an expanding sphere (note that the radii are not to scale and by 740 s there are no molecules on the membrane). (b) An example of a single trajectory showing the number of cytoplasmic molecules versus time for an expanding sphere along with the theoretical value as calculated from Ref. . Note that for each parameter value multiple realizations were run and averaged before being compared to the theoretical value.

FIG. 7.

Diagram describing the process where polarization of the yeast model (spatial psrofile of protein concentration) is used to calculate the deformation of the domain. At each time step of the algorithm the following process is repeated. First the biochemical system is simulated using the spatial stochastic solvers in PyURDME for a length of Δt. Next the point of maximum polarization is found and the normal vector is calculated at that point. Then, the velocity of the surface is calculated using the normal vector as the direction, with the amplitude calculated from a Gaussian function centered at the maximum polarization point (empirically parameterized). The mesh is then deformed by the application of the velocity field. Finally, the biochemical state of the system is transferred to the new mesh.

FIG. 8.

Comparison between microscopy images of yeast cells during polarized growth and simulations of the growing yeast mating projection. (a) Fluorescent microscopy time-lapse images of yeast cells during exposure to mating pheromone (α-factor). Cells are tagged with Mid2-GFP (see Appendix D for experimental details). (b) Manual cell shape extraction overlaid on microscopy images for a single cell. (c) Enlarged cell shape without microscopy image. (d) Scatter plot of the voxel centers of our simulation results projected onto a plane containing the origin and the point of greatest polarization. (e) 3D visualization of the simulated growing yeast cell, where the color map shows the concentration of active Cdc42 on the membrane (red corresponds to the highest concentration, and blue to the least).