Temporally correlated fluctuations drive epileptiform dynamics
- PMID: 27865920
- PMCID: PMC5353705
- DOI: 10.1016/j.neuroimage.2016.11.034
Temporally correlated fluctuations drive epileptiform dynamics
Abstract
Macroscopic models of brain networks typically incorporate assumptions regarding the characteristics of afferent noise, which is used to represent input from distal brain regions or ongoing fluctuations in non-modelled parts of the brain. Such inputs are often modelled by Gaussian white noise which has a flat power spectrum. In contrast, macroscopic fluctuations in the brain typically follow a 1/fb spectrum. It is therefore important to understand the effect on brain dynamics of deviations from the assumption of white noise. In particular, we wish to understand the role that noise might play in eliciting aberrant rhythms in the epileptic brain. To address this question we study the response of a neural mass model to driving by stochastic, temporally correlated input. We characterise the model in terms of whether it generates "healthy" or "epileptiform" dynamics and observe which of these dynamics predominate under different choices of temporal correlation and amplitude of an Ornstein-Uhlenbeck process. We find that certain temporal correlations are prone to eliciting epileptiform dynamics, and that these correlations produce noise with maximal power in the δ and θ bands. Crucially, these are rhythms that are found to be enhanced prior to seizures in humans and animal models of epilepsy. In order to understand why these rhythms can generate epileptiform dynamics, we analyse the response of the model to sinusoidal driving and explain how the bifurcation structure of the model gives rise to these findings. Our results provide insight into how ongoing fluctuations in brain dynamics can facilitate the onset and propagation of epileptiform rhythms in brain networks. Furthermore, we highlight the need to combine large-scale models with noise of a variety of different types in order to understand brain (dys-)function.
Keywords: Epilepsy; Ictogenesis; Jansen-Rit model; Neural mass models; Nonlinear dynamics; Ornstein‐Uhlenbeck noise; Stochastic effects.
Copyright © 2017 The Authors. Published by Elsevier Inc. All rights reserved.
Figures



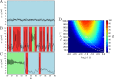
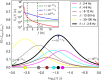
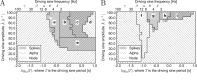
References
-
- Aksenova T.I., Volkovych V.V., Villa A.E.P. Detection of spectral instability in EEG recordings during the preictal period. J. Neural Eng. 2007;4:173–178. - PubMed
-
- Alarcon G., Binnie C.D., Elwes R.D., Polkey C.E. Power spectrum and intracranial EEG patterns at seizure onset in partial epilepsy. Electroencephalogr. Clin. Neurophysiol. 1995;94:326–337. - PubMed
-
- Amari S. Homogeneous nets of neuron-like elements. Biol. Cybern. 1974;17:211–220. - PubMed
-
- Bayer L., Constantinescu I., Perrig S., Vienne J., Vidal P.-P., Mühlethaler M., Schwartz S. Rocking synchronizes brain waves during a short nap. Curr. Biol.: CB. 2011;21:R461–R462. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical

