Eigenspace-based beamformer using oblique signal subspace projection for ultrasound plane-wave imaging

Abstract

Background: The Eigenspace-based beamformers, by orthogonal projection of signal subspace, can remove a large part of the noise, and provide better imaging contrast upon the minimum variance beamformer. However, wrong estimate of signal and noise component may bring dark-spot artifacts and distort the signal intensity. The signal component and noise and interference components are considered uncorrelated in conventional eigenspace-based beamforming methods. In ultrasound imaging, however, signal and noise are highly correlated. Therefore, the oblique projection instead of orthogonal projection should be taken into account in the denoising procedure of eigenspace-based beamforming algorithm.

Methods: In this paper, we propose a novel eigenspace-based beamformer based on the oblique subspace projection that allows for consideration of the signal and noise correlation. Signal-to-interference-pulse-noise ratio and an eigen-decomposing scheme are investigated to propose a new signal and noise subspaces identification. To calculate the beamformer weights, the minimum variance weight vector is projected onto the signal subspace along the noise subspace via an oblique projection matrix.

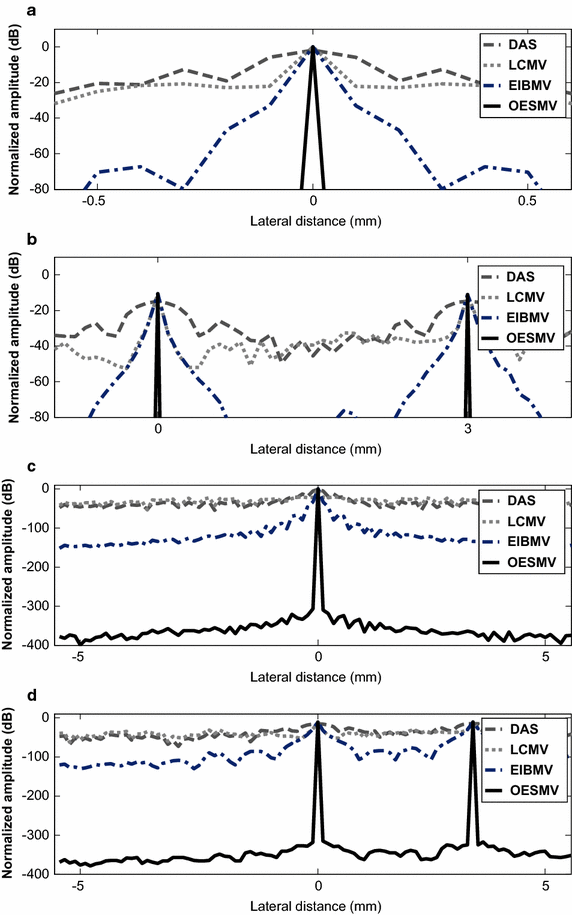
Results: We have assessed the performance of proposed beamformer by using both simulated software and real data from Verasonics system. The results have exhibited the improved imaging qualities of the proposed beamformer in terms of imaging resolution, speckle preservation, imaging contrast, and dynamic range.

Conclusions: Results have shown that, in ultrasound imaging, oblique projection is more sensible and effective than orthogonal subspace projection. Better signal and speckle preservation could be obtained by oblique projection compare to orthogonal projection. Also shadowing artifacts around the hyperechoic targets have been eliminated. Implementation the new subspace identification has enhanced the imaging resolution of the minimum variance beamformer due to the increasing the signal power in direction of arrival. Also it has offered better sidelobe suppression and a higher dynamic range.

Keywords: Beamforming; Eigenspace-based minimum variance; Oblique projection matrix; Signal subspace; Ultrasound plane-wave imaging.

Fig. 1

The beamformed response for simulated point targets, with 80 dB dynamic range. a The DAS, b the LCMV, c the EIBMV (∂ = 0.9) and d the OESMV (∂ = 0.9, η = 0.05, τ = 0.2)

Fig. 2

Lateral deviation of simulated point targets at the depth. a and c z = 20 mm, b and d z = 40 mm. a, b are shown with -80 dB and c, d with -400 dynamic ranges

Fig. 3

The beamformed response for the simulated cyst with a 80 dB dynamic range. a The DAS, b the LCMV, c the EIBMV (∂ = 0.03), d the EIBMV (∂ = 0.13) and e the OESMV (∂ = 0.03, η = 0.05, τ = 0.2)

Fig. 4

Lateral deviation of simulated cyst at the depth z = 35 mm

Fig. 5

The beamformed response for the simulated cyst with a 200 dB dynamic range. a The EIBMV (∂ = 0.03), b the OESMV (∂ = 0.03, η = 0.05, τ = 0.2)

Fig. 6

The beamformed response for the real wire phantom with 80 dB dynamic range. a The DAS, b the LCMV, c the EIBMV (∂ = 0.16), d the OESMV (∂ = 0.16, η = 0.05), e the EIBMV (∂ = 0.01), and f the OESMV (∂ = 0.01, η = 0.05, τ = 0.12)

Fig. 7

Lateral deviation of real point target at the depth z = 40 mm. The OSBMV, in both small and large straightforward thresholding has a narrower mainlobe at −6 dB narrower than that by the LCMV and the EIBMV

Fig. 8

The beamformed response for the real cyst with 80 dB dynamic range. a The DAS, b the LCMV, c the EIBMV (∂ = 0.26), d the EIBMV (∂ = 0.3) and e the OESMV (∂ = 0.26, η = 0.05, τ = 0.11)