A Biophysical Model for Cytotoxic Cell Swelling

Abstract

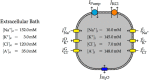
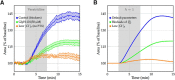
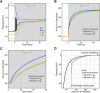
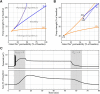
We present a dynamic biophysical model to explain neuronal swelling underlying cytotoxic edema in conditions of low energy supply, as observed in cerebral ischemia. Our model contains Hodgkin-Huxley-type ion currents, a recently discovered voltage-gated chloride flux through the ion exchanger SLC26A11, active KCC2-mediated chloride extrusion, and ATP-dependent pumps. The model predicts changes in ion gradients and cell swelling during ischemia of various severity or channel blockage with realistic timescales. We theoretically substantiate experimental observations of chloride influx generating cytotoxic edema, while sodium entry alone does not. We show a tipping point of Na⁺/K⁺-ATPase functioning, where below cell volume rapidly increases as a function of the remaining pump activity, and a Gibbs-Donnan-like equilibrium state is reached. This precludes a return to physiological conditions even when pump strength returns to baseline. However, when voltage-gated sodium channels are temporarily blocked, cell volume and membrane potential normalize, yielding a potential therapeutic strategy.

Significance statement: Cytotoxic edema most commonly results from energy shortage, such as in cerebral ischemia, and refers to the swelling of brain cells due to the entry of water from the extracellular space. We show that the principle of electroneutrality explains why chloride influx is essential for the development of cytotoxic edema. With the help of a biophysical model of a single neuron, we show that a tipping point of the energy supply exists, below which the cell volume rapidly increases. We simulate realistic time courses to and reveal critical components of neuronal swelling in conditions of low energy supply. Furthermore, we show that, after transient blockade of the energy supply, cytotoxic edema may be reversed by temporary blockade of Na⁺ channels.

Keywords: ATP; Gibbs–Donnan equilibrium; cytotoxic edema; electrodiffusion; osmosis.

Figure 1.

Schematic model overview with typical ion concentrations. Negatively charged, impermeant macromolecules are denoted by A⁻. Leak and voltage-gated ion channels (yellow) yield ion currents that are balanced by the electrogenic ATP-dependent Na⁺/K⁺ pump (cyan) and the electroneutral KCl cotransporter (orange). While the pump moves both Na⁺ and K⁺ against their electrochemical gradients and therefore needs ATP to run, the KCl cotransporter uses the energy stored in the standing transmembrane gradient of K⁺ to move Cl⁻ out of the cell. Any difference in osmolarity between the intracellular and extracellular space will yield a water flux across the membrane (blue), changing the cell volume.

Figure 2.

Voltage-gated chloride current through the ion exchanger SLC26A11. Marks denote voltage-clamp recordings of the transmembrane current blocked by application of DIDS in coronal brain slices of rats, reported in the study by Rungta et al. (2015; Fig. 7D). Error bars represent the SEM. Raw data were provided by the Brian MacVicar laboratory. Dashed lines depict the modeled voltage-gated chloride current ICl−G for normal ([Cl−]e = 135 mm and low [Cl−]e = 10.5 mm extracellular and corresponding resting intracellular chloride concentrations.

Figure 3.

Neuronal swelling after the application of veratridine. A, Experimental data of neuronal swelling in hippocampal and cortical brain slices of rats with mean and SEM, reported in the study by Rungta et al. (2015; Figs. 3F, 6E). Bath application of veratridine is indicated by a shaded area. Control resembles a blocker cocktail of APV, CNQX, Cd2⁺, and picrotoxin (PTX). Swelling is inhibited by the SLC26A11 blocker GlyH-101 and is largely prevented by reducing extracellular chloride concentration to 10.5 mm. Raw data were provided by the Brian MacVicar laboratory. In the low [Cl]_e experiments, the lack of the GABA_A receptor blocker PTX leads to an additional chloride influx, which is not taken into account in the model. B, Model simulations closely mimic experimental results. The application of veratridine is modeled by blocking the sodium inactivation gate. Shown are default parameter values, blockade of the voltage-gated chloride current modeling the effect of GlyH-101, and low extracellular chloride [Cl⁻]_e of 10.5 mm. Swelling is triggered by a very small and brief excitatory sodium current at t = 2.5 min. For calculation of the cross-section area, we assume that neurons are spherical. The water permeability of the cell membrane is identical in all three conditions.

Figure 4.

Illustration of the Gibbs–Donnan equilibrium for different extracellular bath solutions. A, For a bath solution resembling brain interstitial fluid under physiological conditions, the Gibbs–Donnan equilibrium is associated with a Gibbs–Donnan potential of V_GD = −11.3 mV and a large total solute concentration gradient of Δ[S] = [S]_i − [S]_e = 163.0 mm. B, C, Iso-osmotic replacement of extracellular chloride and sodium by cell membrane-impermeant anions A⁻ and cations B⁺, respectively, leads to a significant reduction of the total ion concentration gradient Δ[S], and therefore osmotic pressure, in Gibbs–Donnan equilibrium. Qualitative estimates of associated changes in cell volume are indicated with a dashed line. Note that in all situations electroneutrality is preserved and that [Cl⁻]_i defines the osmotic pressure.

Figure 5.

Convergence toward Gibbs–Donnan equilibrium and subsequent cell swelling after blocking the Na⁺/K⁺-ATPase, simulating ouabain perfusion or OGD. A, Membrane depolarization and evolution of Nernst potentials for default parameters. After blocking the Na⁺/K⁺-ATPase, the neuron starts spiking for ∼1 min (illustrated by a filled black region), terminating in depolarization block. B, Time course of the increase in cell volume using blockers for the transient sodium current (simulating the effect of TTX) or voltage-gated chloride current (simulating the effect of GlyH-101 or DIDS). In both conditions, neuronal swelling is slowed down, but the final cell volume is not affected. C, Closeup of the volume dynamics during the first 90 min after shutdown of the Na⁺/K⁺-ATPase. Blockade of the transient sodium current prevents spiking and slows down the depolarization of the cell, which yields a delay in the opening of the voltage-gated chloride channel. Blockade of the voltage-gated chloride current limits the chloride flux and therefore the water flux into the cell. D, Convergence from the physiological resting state toward the osmotically balanced Gibbs–Donnan equilibrium (both denoted by marks). Fast voltage fluctuations due to spiking are averaged out. While converging toward the branch of Gibbs–Donnan equilibria (solid black line), swelling speeds up once the voltage-gated chloride current gets activated (Fig. 2).

Figure 6.

Bifurcation diagram with the Na⁺/K⁺-ATPase strength as a free parameter. A, Stable equilibria are denoted by a solid line, and unstable equilibria are denoted by a dotted line. At ∼65% of the baseline pump strength, the physiological resting state disappears via a saddle-node bifurcation (SN; orange). For lower values of the pump strength, the cell will converge to a depolarized Gibbs–Donnan-like equilibrium. This pathological state is stable for pump strengths of up to ∼185% of the baseline pump rate, where it loses stability due to a subcritical Hopf bifurcation (H; blue). B, The cell volume is almost constant in the physiological equilibrium branch, but is highly dependent on the pump strength in the pathological equilibrium branch, where minor differences in the remaining pump rate cause major differences in equilibrium cell size.

Figure 7.

Bistability for physiological pump strengths. A, Continuation of the saddle-node (orange) and Hopf (blue) bifurcation (denoted by the two marks) with the maximal transient sodium permeability as an additional free parameter. Bifurcation of stable equilibria are denoted by a solid line, and bifurcations of unstable equilibria are denoted by a dotted line and are shown for completeness. The region of bistability between the solid lines shrinks with decreasing sodium permeability. B, Magnification with codimension-two bifurcations. The two branches of saddle-node bifurcations meet in a cusp singularity (CP). To the left of this point, the model transitions smoothly between the physiological and pathological state. The Hopf bifurcation curve intersects a saddle-node branch at a zero-Hopf point (ZH) and undergoes a generalized Hopf bifurcation (GH), becoming supercritical. C, Model simulation illustrating bistability and a possible way to return to the physiological resting state. Transition to the pathological equilibrium is induced by a 10 min blockade of the Na⁺/K⁺-ATPase (simulating ouabain perfusion or oxygen-glucose deprivation). After temporary blocking of the voltage-gated sodium channels (simulating the effect of, e.g., TTX), the neuron returns to its physiological equilibrium.