Thermally induced magnetic relaxation in square artificial spin ice

Abstract

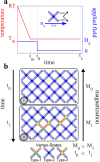
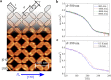
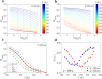
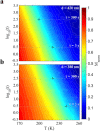
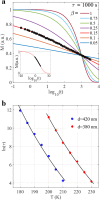
The properties of natural and artificial assemblies of interacting elements, ranging from Quarks to Galaxies, are at the heart of Physics. The collective response and dynamics of such assemblies are dictated by the intrinsic dynamical properties of the building blocks, the nature of their interactions and topological constraints. Here we report on the relaxation dynamics of the magnetization of artificial assemblies of mesoscopic spins. In our model nano-magnetic system - square artificial spin ice - we are able to control the geometrical arrangement and interaction strength between the magnetically interacting building blocks by means of nano-lithography. Using time resolved magnetometry we show that the relaxation process can be described using the Kohlrausch law and that the extracted temperature dependent relaxation times of the assemblies follow the Vogel-Fulcher law. The results provide insight into the relaxation dynamics of mesoscopic nano-magnetic model systems, with adjustable energy and time scales, and demonstrates that these can serve as an ideal playground for the studies of collective dynamics and relaxations.

Figure 1. Relaxation measurement protocol.

(a) The temperature and applied field evolution during the measurement protocol. Starting at room temperature (RT), where the array is in a superparamagnetic state, the external field, H_a, is switched on in the [110]-direction (see inset in (a)) of the array and the cooling starts. As the array is cooled the magnetization of the islands aligns with the applied field. The flipping rate of the islands is suppressed by the applied field and the low temperature. The cooling is halted at the desired measurement temperature (T_m) and stabilized there from t_m to t₀. At t₀ the applied magnetic field is switched off and the relaxation measurements start from a completely dressed array configuration of Type-2 states (I). After the field is switched off the islands can undergo reversals and thereby reduce the magnetization of the array (II). Following the initial reversals the magnetic configuration of the array further relaxes forming strings. Three out of sixteen possible vertex states (Type-1, Type-2 and Type-3) are shown in (b).

Figure 2. Array structure and magnetic characterization.

(a) Atomic force microscopy image of the d = 380 nm array with an overlay showing the patterned geometry of the array. The elongated islands are stadium shaped with l = 330 nm and w = 150 nm. The islands are placed in a square lattice architecture with periodicities of 380 nm (shown) and 420nm (not shown). The different perodicities lead to difference in the magnetic interaction between the islands in the arrays, with the d = 380 nm array being stronger interacting. (b,c) show the magnetic response of the d = 380 nm array as a function of temperature. (b) M_TRM(T) measured after cooling in fields of different strength. As can be seen there is hardly any difference between the different curves indicating that the array starts from a fully dressed state [see Fig. 1 (I)] already at the lowest field, 800 A/m. (c) The dependence of the M_TRM(T) on the heating rate. The onset of decay of the collective array magnetization is shifted to higher temperatures when using a higher heating rate (i.e. a shorter observation time).

Figure 3. Magnetic relaxation.

Normalized magnetization as a function of time for different temperatures as indicated by the color bar for (a) the d = 420 nm array and (b), the d = 380 nm array. (c) Normalized magnetization as a function of temperature for different observation times for the d = 420 nm array. The points are selected by choosing data points along the vertical grey lines in (a), which correspond to specific observation times. The solid line in (c) corresponds to a DC M vs. T measurement of the d = 420 nm array, the observation time of this DC measurement is 30 s. (d) The relaxation rate, S = dM/d log₁₀(t), determined from (a,b), at 300 s as a function of temperature. The minimum corresponds to the maximum relaxation rate and could be taken as an effective blocking temperature for t = 300 s.

Figure 4. Temperature and time dependence of the magnetic relaxation.

Color maps of the magnetization as a function of time and temperature for (a) the d = 420 nm and (b) the d = 380 nm array. In both color maps a strong connection between the time and temperature is observed as stripe like features. This implies that a given magnetization value can be found using several combinations of time and temperature. The contour density along the gray lines for t = 300 s corresponds to the relaxation rates shown in Fig. 3d. The maps further highlight the effect of the observation time on the temperature shift of the maximum for the relaxation rate, as indicated by the crosses for the case of t = 3 s and t = 300 s.

Figure 5. Stretched exponentials and fitting of M_TRM(T) and τ(T).

(a) The variation of a stretched exponential, M = M₀ exp[−(t/τ)^β], for different values of β using a relaxation time τ = 1000 s. The black dots correspond to the recorded relaxation data for the d = 420 nm array at 200 K. In the inset the same data is fitted to a stretched exponential with β ≈ 0.15 and τ ≈ 1000 s, in the time window 10⁻¹⁰ (0.1 ns) to 10¹⁰ s (≈300 years) which covers the majority of the relaxation from M₀ to zero magnetization. The magnetization is normalized to M₀, which is the magnetization directly after the field is switched off (t = t₀), corresponding to a fully dressed state of the array, see Fig. 1 (I). (b) A fit of the temperature dependence of the relaxation time τ to the Vogel Fulcher law, τ = τ₀ exp(E_B/k_B(T − T₀)), for both arrays, yielding an average energy barrier of E_B/k_B = 4500 K.