Allostatic Self-efficacy: A Metacognitive Theory of Dyshomeostasis-Induced Fatigue and Depression
- PMID: 27895566
- PMCID: PMC5108808
- DOI: 10.3389/fnhum.2016.00550
Allostatic Self-efficacy: A Metacognitive Theory of Dyshomeostasis-Induced Fatigue and Depression
Abstract
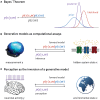
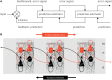
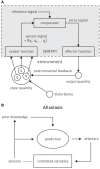
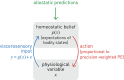
This paper outlines a hierarchical Bayesian framework for interoception, homeostatic/allostatic control, and meta-cognition that connects fatigue and depression to the experience of chronic dyshomeostasis. Specifically, viewing interoception as the inversion of a generative model of viscerosensory inputs allows for a formal definition of dyshomeostasis (as chronically enhanced surprise about bodily signals, or, equivalently, low evidence for the brain's model of bodily states) and allostasis (as a change in prior beliefs or predictions which define setpoints for homeostatic reflex arcs). Critically, we propose that the performance of interoceptive-allostatic circuitry is monitored by a metacognitive layer that updates beliefs about the brain's capacity to successfully regulate bodily states (allostatic self-efficacy). In this framework, fatigue and depression can be understood as sequential responses to the interoceptive experience of dyshomeostasis and the ensuing metacognitive diagnosis of low allostatic self-efficacy. While fatigue might represent an early response with adaptive value (cf. sickness behavior), the experience of chronic dyshomeostasis may trigger a generalized belief of low self-efficacy and lack of control (cf. learned helplessness), resulting in depression. This perspective implies alternative pathophysiological mechanisms that are reflected by differential abnormalities in the effective connectivity of circuits for interoception and allostasis. We discuss suitably extended models of effective connectivity that could distinguish these connectivity patterns in individual patients and may help inform differential diagnosis of fatigue and depression in the future.
Keywords: active inference; allostasis; computational psychiatry; dynamic causal modeling; effective connectivity; homeostasis; multiple sclerosis; predictive coding.
Figures

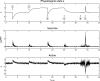
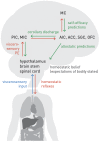
References
-
- Aertsen A., Preißl H. (1999). Dynamics of activity and connectivity in physiological neuronal networks, in Nonlinear Dynamics and Neuronal Networks, ed Schuster H. (New York, NY: Schuster VCH Publishers; ), 281–302.
LinkOut - more resources
Full Text Sources
Other Literature Sources
Molecular Biology Databases

