How does epistasis influence the response to selection?
- PMID: 27901509
- PMCID: PMC5176114
- DOI: 10.1038/hdy.2016.109
How does epistasis influence the response to selection?
Abstract
Much of quantitative genetics is based on the 'infinitesimal model', under which selection has a negligible effect on the genetic variance. This is typically justified by assuming a very large number of loci with additive effects. However, it applies even when genes interact, provided that the number of loci is large enough that selection on each of them is weak relative to random drift. In the long term, directional selection will change allele frequencies, but even then, the effects of epistasis on the ultimate change in trait mean due to selection may be modest. Stabilising selection can maintain many traits close to their optima, even when the underlying alleles are weakly selected. However, the number of traits that can be optimised is apparently limited to ~4Ne by the 'drift load', and this is hard to reconcile with the apparent complexity of many organisms. Just as for the mutation load, this limit can be evaded by a particular form of negative epistasis. A more robust limit is set by the variance in reproductive success. This suggests that selection accumulates information most efficiently in the infinitesimal regime, when selection on individual alleles is weak, and comparable with random drift. A review of evidence on selection strength suggests that although most variance in fitness may be because of alleles with large Nes, substantial amounts of adaptation may be because of alleles in the infinitesimal regime, in which epistasis has modest effects.
Figures

 . Sparse pairwise epistasis is represented by choosing a fraction 1/M of pairwise interactions, ωι j, from a normal distribution with s.d.
. Sparse pairwise epistasis is represented by choosing a fraction 1/M of pairwise interactions, ωι j, from a normal distribution with s.d.  . The trait is now defined as z=δ.γ+δ.ω.δT, where δ=±(1/2). Initial allele frequencies are drawn from a U-shaped β-distribution, mean p̂=0.2 and variance 0.2 p̂q̄. Individuals are produced by Wright–Fisher sampling from parents chosen with probability proportional to W=eβ z. For each example, three sets of allelic and epistatic effects are drawn and for each of those, three populations are evolved; this gives 9 replicates in all.
. The trait is now defined as z=δ.γ+δ.ω.δT, where δ=±(1/2). Initial allele frequencies are drawn from a U-shaped β-distribution, mean p̂=0.2 and variance 0.2 p̂q̄. Individuals are produced by Wright–Fisher sampling from parents chosen with probability proportional to W=eβ z. For each example, three sets of allelic and epistatic effects are drawn and for each of those, three populations are evolved; this gives 9 replicates in all.



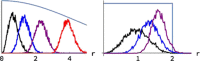


 , plotted against initial allele frequency, p0 (left and middle respectively). The right plot shows the ratio between the information gain and the expected total fitness variance. Selection strength is 4Nes=α=0.125, 0.25,…, 8 (black…red). In the limit α→0, the scaled ratio tends to 1/16, independent of p0. A full colour version of this figure is available at the Heredity journal online.
, plotted against initial allele frequency, p0 (left and middle respectively). The right plot shows the ratio between the information gain and the expected total fitness variance. Selection strength is 4Nes=α=0.125, 0.25,…, 8 (black…red). In the limit α→0, the scaled ratio tends to 1/16, independent of p0. A full colour version of this figure is available at the Heredity journal online.References
-
- Barton NH. (1989). The divergence of a polygenic system under stabilising selection, mutation and drift. Genet Res 54: 59–77. - PubMed
-
- Barton NH, Etheridge AM, Veber A. (2016) . The infinitesimal model http://biorxiv.org/content/early/2016/02/15/039768.
-
- Bourguet D. (1999). The evolution of dominance. Heredity 83: 1–4. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

