Water striders adjust leg movement speed to optimize takeoff velocity for their morphology

Abstract

Water striders are water-walking insects that can jump upwards from the water surface. Quick jumps allow striders to avoid sudden dangers such as predators' attacks, and therefore their jumping is expected to be shaped by natural selection for optimal performance. Related species with different morphological constraints could require different jumping mechanics to successfully avoid predation. Here we show that jumping striders tune their leg rotation speed to reach the maximum jumping speed that water surface allows. We find that the leg stroke speeds of water strider species with different leg morphologies correspond to mathematically calculated morphology-specific optima that maximize vertical takeoff velocity by fully exploiting the capillary force of water. These results improve the understanding of correlated evolution between morphology and leg movements in small jumping insects, and provide a theoretical basis to develop biomimetic technology in semi-aquatic environments.

Figure 1. Jumping of a water strider.

(a) A water strider (male Aquarius paludum with a body mass of 37.2 mg and an average length of middle and hind legs of 22.1 mm) that rests and jumps on water. (b–d) Definitions of various lengths considered in this study. (b) The vertical lengths including body centre location y, vertical distance from the tip of the legs to the horizontal plane through body centre l_s and dimple depth h. (c) The lengths of legs including the radius r, and the length of tibia plus tarsus l_t. (d) The wetted length of the leg l_w. (e) A representative sequence of the jump of the water strider on the water surface. (f–h) Measurement data extracted from a movie corresponding to e. (f) Average dimple depth formed by the right and left legs (open circles for middle legs, filled circles for hind legs) during the jump. Error bars indicate standard deviation between right and left legs. (g) Vertical velocity of the body centre ν (open circles) and the average downward velocity of the four legs with respect to the horizontal plane through the body centre ν_s (filled circles). Error bars indicate standard deviation among four legs. (h) Height of the body centre of the water strider during the jump. The vertical blue bar in f–h indicates the moment when the dimple reaches the maximal depth (the panel corresponding to 13 ms in e shows the dimple that reached maximal depth). Body velocity profile in g is the same data as that of water strider 2 in Koh et al.

Figure 2. Comparison of empirical and modelled leg movements.

The solid lines correspond to the model assuming the sinusoidal model of leg rotation and the circles correspond to the average of measurement of four legs from the same movie used in Fig. 1e–h. The error bars indicate standard deviation among the four legs. (a) The average vertical distance between the body centre and distal end of legs (l_s) across the leg rotation cycle. (b) The average downward velocity of four legs with respect to body centre (ν_s). (c) The average time derivative of the angle of legs with respect to the horizontal plane (). 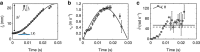The dashed line indicates the time average of the measured values of through the whole cycle and the solid line refers to the corresponding angular speed of leg rotation ω used in the model calculations of l_s and ν_s in a,b.

Figure 3. Different jump modes.

(a) Schematic representation of three modes of jump: pre-takeoff closing, post-takeoff closing and meniscus breaking jumps. (b,c) Enlarged images of the leg and dimple in a post-takeoff closing jump (h_m=2.5 mm) and a meniscus breaking jump (h_m>3.9 mm): (b) the leg that does not reach the sinking depth leaves the surface unpenetrated, (c) the leg pierces the surface just below the sinking depth. The red arrow at 3 ms indicates the rupture point of the water surface. The pre-takeoff closing jump was not observed in the experiments.

Figure 4. Theoretical and empirical results of jumping of water striders.

(a–c) Effect of the dimensionless angular velocity of the leg Ω and the dimensionless maximum downward reach of leg L on takeoff velocity ν_t with warmer colours indicating higher takeoff velocity for water strider species of three different sizes expressed in different values of the variable M: M=0.1 in a; M=0.5 in b; M=2.0 in c. M represents the ratio of body mass to the maximal mass of water that the legs can displace by pushing against the water surface. Water striders observed in this study have M near 0.5. The arrows in a show that the longer leg indicated by red arrows should move slower, for example, than the leg indicated black arrows to get maximum takeoff speed. (d–f) Effect of the dimensionless angular velocity of the leg Ω and the dimensionless maximum downward reach of legs L on the time taken to escape from water t_t with warmer colours indicating longer escape time corresponding to the conditions of a–c, respectively. White dashed lines indicate the boundary of meniscus breaking jump. (g) Phase diagram for the three jump modes as a function of ΩM^1/2 and L: post-takeoff closing (white area), pre-takeoff closing (light shaded area), and meniscus breaking (dark shaded area). The red lines marked with I, II and III indicate the conditions resulting in maximal vertical takeoff velocity with three M in a–c: I with M=0.1; II with M=0.5; III with M=2.0. The dashed line shows the line of ΩM^1/2=4/L+0.1. The phase diagram includes empirical results from the jump characteristics of females (filled symbols) and males (unfilled symbols) of G. remigis (inverted triangles), G. comatus (diamonds), G. latiabdominis (circles), G. gracilicornis (triangles) and A. paludum (squares) with nymph of G. remigis (stars).