Electric-field-stimulated protein mechanics
- PMID: 27926732
- PMCID: PMC5730412
- DOI: 10.1038/nature20571
Electric-field-stimulated protein mechanics
Abstract
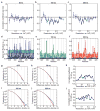
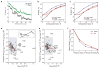
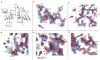
The internal mechanics of proteins-the coordinated motions of amino acids and the pattern of forces constraining these motions-connects protein structure to function. Here we describe a new method combining the application of strong electric field pulses to protein crystals with time-resolved X-ray crystallography to observe conformational changes in spatial and temporal detail. Using a human PDZ domain (LNX2PDZ2) as a model system, we show that protein crystals tolerate electric field pulses strong enough to drive concerted motions on the sub-microsecond timescale. The induced motions are subtle, involve diverse physical mechanisms, and occur throughout the protein structure. The global pattern of electric-field-induced motions is consistent with both local and allosteric conformational changes naturally induced by ligand binding, including at conserved functional sites in the PDZ domain family. This work lays the foundation for comprehensive experimental study of the mechanical basis of protein function.
Conflict of interest statement
The authors declare no competing financial interests.
Figures


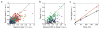






References
-
- Alberts B. The cell as a collection of protein machines: preparing the next generation of molecular biologists. Cell. 1998;92:291–294. - PubMed
-
- Méndez J, Stillman B. Perpetuating the double helix: molecular machines at eukaryotic DNA replication origins. BioEssays. 2003;25:1158–1167. - PubMed
-
- Boehr DD, McElheny D, Dyson HJ, Wright PE. The dynamic energy landscape of dihydrofolate reductase catalysis. Science. 2006;313:1638–1642. - PubMed
-
- Noji H, Yasuda R, Yoshida M, Kinosita K., Jr Direct observation of the rotation of F1-ATPase. Nature. 1997;386:299–302. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

