Challenges in Species Tree Estimation Under the Multispecies Coalescent Model

Abstract

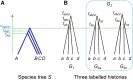
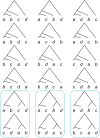
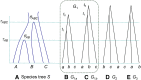
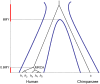
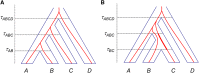
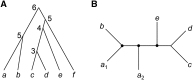
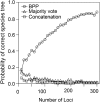
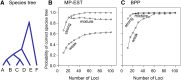
The multispecies coalescent (MSC) model has emerged as a powerful framework for inferring species phylogenies while accounting for ancestral polymorphism and gene tree-species tree conflict. A number of methods have been developed in the past few years to estimate the species tree under the MSC. The full likelihood methods (including maximum likelihood and Bayesian inference) average over the unknown gene trees and accommodate their uncertainties properly but involve intensive computation. The approximate or summary coalescent methods are computationally fast and are applicable to genomic datasets with thousands of loci, but do not make an efficient use of information in the multilocus data. Most of them take the two-step approach of reconstructing the gene trees for multiple loci by phylogenetic methods and then treating the estimated gene trees as observed data, without accounting for their uncertainties appropriately. In this article we review the statistical nature of the species tree estimation problem under the MSC, and explore the conceptual issues and challenges of species tree estimation by focusing mainly on simple cases of three or four closely related species. We use mathematical analysis and computer simulation to demonstrate that large differences in statistical performance may exist between the two classes of methods. We illustrate that several counterintuitive behaviors may occur with the summary methods but they are due to inefficient use of information in the data by summary methods and vanish when the data are analyzed using full-likelihood methods. These include (i) unidentifiability of parameters in the model, (ii) inconsistency in the so-called anomaly zone, (iii) singularity on the likelihood surface, and (iv) deterioration of performance upon addition of more data. We discuss the challenges and strategies of species tree inference for distantly related species when the molecular clock is violated, and highlight the need for improving the computational efficiency and model realism of the likelihood methods as well as the statistical efficiency of the summary methods.

Keywords: BPP; anomaly zone; concatenation; gene trees; incomplete lineage sorting; maximum likelihood; multispecies coalescent; species trees.

Figure 1

(A) Asymmetrical species tree (S) for four species and (B) symmetrical and asymmetrical gene trees (G₁ and G₂). When the two internal branch lengths in the species tree are ≈0, all three coalescent events on the gene tree occur in the common ancestor ABCD, so that all 18 labeled histories have equal probabilities ($\frac{1}{18}$) (Figure. 2), with P(G₂) ≈ 2P(G₁). When the internal branch lengths are nonzero but very small, it is possible to have P(G₂) > P(G₁), in which case the species tree S is in the anomaly zone.

Figure 2

The 18 labeled histories for four sequences sampled from a population (a, b, c, d), with the node ages drawn to reflect the expectations of the coalescent times. A labeled history is a rooted tree with the interior nodes rank-ordered by age. Thus the rooted tree ((a, b), (c, d)) corresponds to two labeled histories, depending on whether sequences a and b coalesce before or after sequences c and d. Under the coalescent model, all possible labeled histories (but not the rooted trees) have equal probabilities. For four sequences, each of the 12 asymmetrical rooted trees is compatible with only one labeled history and has probability 1/18, while each of the three symmetrical rooted trees is compatible with two labeled histories and has probability 2/18.

Figure 3

(A) The species tree ((A, B), C) for three species, showing the parameters in the MSC model, Θ = {τ_ABC, τ_AB, θ_ABC, θ_AB}. Both τs and θs are measured by the expected number of mutations per site. If multiple sequences are sampled for the same locus from the same species (say, A), the population size parameter for that species (say, θ_A) will also be a parameter. (B–E) The possible gene trees for a locus with three sequences (a, b, c), one sequence from each species. Under the MSC, gene trees G_1b, G₂, and G₃ have the same probability, so that the species tree-gene tree mismatch probability is P_SG = P(G₂) + P(G₃) = 1−P(G₁).

Figure 4

The MSC assumes that all sites at the same locus share the same gene tree (topology and branch lengths). This assumption is valid if there is no recombination around the time periods when coalescent events occur (highlighted by thick bars on the time axis), even though recombination may occur in other parts of the gene tree, when there is only one sequence ancestral to the sample in a population. In the example, humans and chimpanzees diverged at 6 MA, while the MRCA for the human sample is at 0.6 MA. Recombination events over the time period (0.6, 6) do not affect the MSC density of gene trees.

Figure 5

Deep coalescence, marked by thick segment of a gene-tree branch, means that two or more lineages pass through an ancestral species when one traces the gene genealogy backward in time (Maddison 1997). The given rooted gene tree, (((a, b), c), d), is fitted to two species trees: (((A, B), C), D) in (A) and ((A, (B, C)), D) in (B). In (A), at most one lineage leaves each ancestral species so that the number of deep coalescence is 0. In (B), two lineages (sequences b and c) pass ancestral species BC and one of them is counted as a deep coalescence. The method of minimum deep coalescence for species tree estimation (MDC) minimizes the total number of deep coalescence over all gene trees.

Figure 6

Gene tree topologies can be used to define a distance between two species and the resulting distance matrix can be used to construct the species tree using, e.g., NJ (Saitou and Nei 1987). (A) In the STAR method (for species tree estimation using average ranks of coalescences, Liu et al. 2009), the distance between two species is defined as the rank of the ancestral node for the two species on the rooted gene tree. In the example tree, species A and B have the distance or rank 5, while species A and C have the rank 6. The rank for the root is the number of sequences, and the rank decreases from the root to the tips of the gene tree. Note that distantly related species tend to have large distances or ranks. A distance matrix is constructed by averaging the ranks across all gene trees, and then analyzed using NJ (Liu et al. 2009). (B) The NJ_st method (Liu and Yu 2011) uses the gene-tree internode distance, defined as the number of internal nodes in the unrooted gene tree between the two species. If multiple sequences are sampled from the same species, the internode distance is averaged across all pairs from the two species. In the example, the internode distance is 3 between species B and E and is 1.5 between A and B. The matrix of average internode distances between species (averaged across loci) is used to construct a species tree using NJ.

Figure 7

Species tree inference in the anomaly zone. The probability of inferring the correct species tree by majority-vote, concatenation, and BI (bpp), plotted against the number of loci (L).

Figure 8

More data for worse performance for five species? The probability of inferring (A) the correct species tree for five species by (B) mp-est and (C) bpp using weak genes only, strong genes only, and a mixture of 20 strong genes plus a number of weak genes. The divergence times on the species tree are τ_AB = τ_CD = 0.002, τ_ABCD = 0.004, τ_ABCDE = 0.006, and τ_ABCDEF = 0.016, with θ = 0.008 for all populations. The number of replicates is 1000 for mp-est and 100 for bpp.

Figure 9

More data for worse performance for three species? The probability of inferring the correct species tree for three species by mp-est, ML (3s), and BI (bpp) using weak genes only, strong genes only, and a mixture of 5 or 10 strong genes plus a number of weak genes. The true species tree is the one in Figure 3A, with τ_ABC = 0.06 and τ_AB = 0.05, and with θ = 0.02 for all populations. The number of replicates is 1000 for 3s and bpp, and ranges from 10⁵ to 10⁷ for mp-est.

Figure 10

More data for worse performance for a toy example of binary data? The species tree is estimated using a summary method that mimics mp-est.