General calibration of microbial growth in microplate readers

Abstract

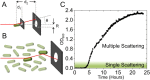
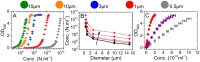
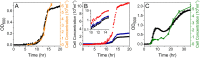
Optical density (OD) measurements of microbial growth are one of the most common techniques used in microbiology, with applications ranging from studies of antibiotic efficacy to investigations of growth under different nutritional or stress environments, to characterization of different mutant strains, including those harbouring synthetic circuits. OD measurements are performed under the assumption that the OD value obtained is proportional to the cell number, i.e. the concentration of the sample. However, the assumption holds true in a limited range of conditions, and calibration techniques that determine that range are currently missing. Here we present a set of calibration procedures and considerations that are necessary to successfully estimate the cell concentration from OD measurements.

Figure 1

Schematic showing that light incident on a sample is scattered by an angle θ from the optical axis (z), either once as in (A) or multiple times (B). Single scattering events are more likely to deflect light away from the aperture (radius R), but the effect of this scattering is highly dependent upon the size of the detector and the distance between detector and sample (d₁ or d₂). As the concentration of cells increases, the probability of light being scattered back into the detector is increased. (C) A typical OD curve for E. coli measured at λ = 600 nm (for measurements at different λ see Supplementary Fig. 2). The depicted curve is the mean value of ten replicate measurements (performed in separate wells of the same plate in the microplate reader and on independent days and separate plates). Error bars are the standard error of the mean. Where the error bars are not visible, they are smaller then the data symbols. Single and multiple scattering regimes have been indicated with different colour shading. The OD saturates when N is large enough to deplete the nutrient sources in the media.

Figure 2. OD measurements of spherical polystyrene bead suspensions.

Each set of data (for a given bead size) consists of dilutions of two independently prepared stock solutions whose actual concentration was determined by counting in a microfluidic slide (Methods). For each independently prepared dilution series at least five experimental replicates were performed and plotted as averages with standard errors. Where independent dilution series were prepared for the same bead size these are plotted with the same colour. The differences between independently prepared and counted dilution series for the same bead size are so small that the data overlap. Any error bars that are not visible are smaller then the data symbols. Bead size corresponds to the diagram above the graphs (0.51 ± 0.01 µm, 0.96 ± 0.07 µm, 3.00 ± 0.07 µm, 10.0 ± 0.6 µm and 15.7 ± 1.4 µm) and bead index of refraction is n_p = 1.59. Representative images of beads used for C measurements are shown in Supplementary Figure 3. (A) Comparison of concentrations (Methods) and measured OD in a microplate reader for a given bead diameter. (B) The bead concentration as a function of D obtained from (A) for the following ODs: 0.05, 0.1, 0.5, 1 and 10. Increasing OD is represented as increasing brightness of red and by the arrow. (C) Measurements of 0.5 µm; 1.0 µm bead suspensions and the resultant (1:1 by volume) mixture in purple.

Figure 3

(A) OD vs. C is shown for yeast diploids (grey); yeast haploid (purple); filamentous (green) and mid-log (black) E. coli; and early (blue) and late (red) stationary phase E. coli using dilutions of at least two cell stock solutions prepared from cells grown on different days. Actual cell concentrations were determined by counting in a microscope. For each independently prepared dilution series at least five experimental replicates were performed and are plotted as averages with standard errors. Independent dilution series that were prepared for the same cell size are plotted with the same colour. For cells of the same size, the differences between independently prepared and counted dilution series are so small that the data overlap. Error bars that are not visible are smaller then the data symbols. (B–H) Representative images of each culture obtained during microscopy. The scale bar is shown in B and applies to all panels. (B) Yeast CLN3Δ homozygous diploid mutant (C) Yeast diploid, (D) Yeast haploid. (E) E. coli cells grown in the presence of sub lethal concentration of ampicillin to induce filamentation. (F) E. coli cells grown to mid log phase in LB (OD = 0.2). (G) E. coli cells at early stationary phase (OD = 2.3), (H) E. coli cells at late stationary phase (after 40 hr).

Figure 4. Growth curves and cell counts.

(A) OD (black) and cell concentration (orange) during growth of E. coli in MM9 with glucose. OD and C are correlated until starvation when cell size is no longer constant. (B) The OD curve from (A) converted to cell concentration using the the mid-log (black), 15 hr (blue) and 40 hr (red) curves in Fig. 3A. Calibration performed on cells of different sizes produces substantial differences in cell concentration. (C) OD (black) and cell concentration (green) in LB with 9 Ampicillin. The lack of correlation between OD and C is caused by antibiotic induced filamentation and filaments of fluctuating length during growth. For (B) and (C), the OD curve shown is an average with standard errors of 10 independent experimental replicates. Each cell concentration point is an average count with the standard error obtained from counting 20–50 independent fields of view in a microscope (Methods).