The Multivariate Temporal Response Function (mTRF) Toolbox: A MATLAB Toolbox for Relating Neural Signals to Continuous Stimuli

Abstract

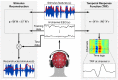
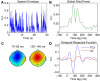
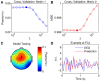
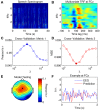
Understanding how brains process sensory signals in natural environments is one of the key goals of twenty-first century neuroscience. While brain imaging and invasive electrophysiology will play key roles in this endeavor, there is also an important role to be played by noninvasive, macroscopic techniques with high temporal resolution such as electro- and magnetoencephalography. But challenges exist in determining how best to analyze such complex, time-varying neural responses to complex, time-varying and multivariate natural sensory stimuli. There has been a long history of applying system identification techniques to relate the firing activity of neurons to complex sensory stimuli and such techniques are now seeing increased application to EEG and MEG data. One particular example involves fitting a filter-often referred to as a temporal response function-that describes a mapping between some feature(s) of a sensory stimulus and the neural response. Here, we first briefly review the history of these system identification approaches and describe a specific technique for deriving temporal response functions known as regularized linear regression. We then introduce a new open-source toolbox for performing this analysis. We describe how it can be used to derive (multivariate) temporal response functions describing a mapping between stimulus and response in both directions. We also explain the importance of regularizing the analysis and how this regularization can be optimized for a particular dataset. We then outline specifically how the toolbox implements these analyses and provide several examples of the types of results that the toolbox can produce. Finally, we consider some of the limitations of the toolbox and opportunities for future development and application.

Keywords: EEG/MEG; reverse correlation; sensory processing; stimulus reconstruction; system identification.

Figure 1

Schematic of the forward and backward modeling approaches implemented by mTRF Toolbox. Stimulus reconstruction (i.e., backward modeling) can be used to decode specific stimulus features from recorded neural response data in order to estimate how accurately this information was encoded in the brain. Temporal response function estimation (i.e., forward modeling) can be used in a similar manner to predict the neural response to a novel stimulus, but also allows for detailed examination of how the stimulus features were encoded in the brain and interpretation of the underlying neural generators.

Figure 2

Univariate TRF estimation. (A) A 30-s segment of the broadband speech envelope. (B) Global field power measured at each time lag. (C) Scalp topographies of the dominant TRF components occurring at ~80 and ~140 ms. The black markers indicate the locations of fronto-central channel, FCz, and occipital channel, Oz. (D) Grand average TRFs at FCz (blue trace) and Oz (red trace).

Figure 3

Optimization of TRFs for EEG prediction. (A) Cross-validation of model based on the correlation between the original and predicted EEG response (Pearson's r averaged across channels and trials). The filled marker indicates the highest r-value, i.e., the optimal ridge value. (B) Cross-validation based on mean squared error (MSE). The optimal ridge value is identified by the lowest MSE-score. (C) Test of the optimized TRF model shows the correlation coefficient at each channel. The black marker indicates the location of channel FCz. (D) Two-second segments of the EEG response at FCz (blue trace) and the corresponding estimate predicted by the optimized TRF model (red trace).

Figure 4

Multivariate TRF estimation and EEG prediction. (A) A 30-s segment of the speech spectrogram. (B) Grand average mTRF at channel FCz. (C) Cross-validation of model based on the correlation between the original and predicted EEG response (Pearson's r averaged across channels and trials). The filled marker indicates the highest r-value, i.e., the optimal ridge value. (D) Cross-validation based on mean squared error (MSE). The optimal ridge value is identified by the lowest MSE-score. (E) Test of the optimized mTRF model shows the correlation coefficient at each channel. The black marker indicates the location of channel FCz. (F) Two-second segments of the EEG response at FCz (blue trace) and the corresponding estimate predicted by the optimized TRF model (red trace).

Figure 5

Stimulus reconstruction. (A) Cross-validation of model based on the correlation between the original and reconstructed speech envelope (Pearson's r averaged across trials). The filled marker indicates the highest r-value, i.e., the optimal ridge value. (B) Cross-validation based on mean squared error (MSE). The optimal ridge value is identified by the lowest MSE-score. (C) Decoder channel weights averaged over time lags between 110 and 130 ms. (D) Two-second segments of the original speech envelope (blue trace) and the corresponding estimate reconstructed by the optimized decoder (red trace). (E) Decoder channel weights transformed to forward model space using the inversion procedure described by Haufe et al. (2014). The black markers indicate the locations of fronto-central channel, FCz, and occipital channel, Oz. (F) Temporal response function obtained by inverting the decoder weights to the forward model domain at FCz (blue trace) and Oz (red trace).

Figure 6

Multimodal TRF estimation. (A) A 30-s segment of the broadband speech envelope. (B) A 30-s segment of the corresponding frame-to-frame visual motion. (C), Grand average envelope TRFs at Fz (blue trace) and Oz (red trace). (D), Grand average motion TRFs at Fz (blue trace) and Oz (red trace). (E) Scalp topography of the dominant envelope TRF component occurring at 78 ms. (F) Scalp topography of the dominant motion TRF component occurring at 117 ms.

Figure 7

Comparison of the temporal response function (TRF) and cross-correlation (XCOR) approach. (A) A 30-s segment of the broadband speech envelope. (B) A 30-s segment of amplitude modulated noise. (C), Autocorrelation of the speech envelope. (D), Autocorrelation of the noise signal. (E) The impulse response to speech at channel FCz estimated using the TRF approach (blue trace) and the cross-correlation approach (red trace). (F) The impulse response to white noise at channel FCz estimated using the TRF approach (blue trace) and the cross-correlation approach (red trace).