Breeding novel solutions in the brain: a model of Darwinian neurodynamics

Abstract

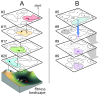
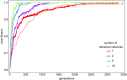
Background: The fact that surplus connections and neurons are pruned during development is well established. We complement this selectionist picture by a proof-of-principle model of evolutionary search in the brain, that accounts for new variations in theory space. We present a model for Darwinian evolutionary search for candidate solutions in the brain. Methods: We combine known components of the brain - recurrent neural networks (acting as attractors), the action selection loop and implicit working memory - to provide the appropriate Darwinian architecture. We employ a population of attractor networks with palimpsest memory. The action selection loop is employed with winners-share-all dynamics to select for candidate solutions that are transiently stored in implicit working memory. Results: We document two processes: selection of stored solutions and evolutionary search for novel solutions. During the replication of candidate solutions attractor networks occasionally produce recombinant patterns, increasing variation on which selection can act. Combinatorial search acts on multiplying units (activity patterns) with hereditary variation and novel variants appear due to (i) noisy recall of patterns from the attractor networks, (ii) noise during transmission of candidate solutions as messages between networks, and, (iii) spontaneously generated, untrained patterns in spurious attractors. Conclusions: Attractor dynamics of recurrent neural networks can be used to model Darwinian search. The proposed architecture can be used for fast search among stored solutions (by selection) and for evolutionary search when novel candidate solutions are generated in successive iterations. Since all the suggested components are present in advanced nervous systems, we hypothesize that the brain could implement a truly evolutionary combinatorial search system, capable of generating novel variants.

Keywords: Darwinian dynamics; attractor network; autoassociative neural network; evolutionary search; learning; neurodynamics; problem solving.

Figure 1.

A) Architecture of multiple attractor networks performing Darwinian search. Boxed units are attractor networks. Each network consists of N neurons ( N = 5 in the figure, represented as black dots). Each neuron receives input from the top (1) and generates output at the bottom (2). Each neuron projects recurrent collaterals to all other neurons (but not to itself), forming thus N × ( N – 1) synapses. The weight matrix of the synapses is represented here as a checkerboard-like matrix, where different shades indicate different connection weights. Selection and replication at the population level is as follows: 1) Each network receives a different noisy copy of the input pattern. 2) According to its internal attractor dynamics, each network returns an output pattern. 3) All output patterns are pooled in the implicit working memory (grey box with dashed outline), where they are evaluated and a fitness w _i is assigned to the i ^th pattern. 4) The best pattern(s) is selected based on fitness. 5) One of the networks is randomly chosen to learn the pattern that was selected, with additional noise (dashed arrow). 6) The selected pattern is copied back to the networks as input to provoke them to generate the next generation of output patterns. B) Lifecycle of candidate solution patterns during a cognitive task. Patterns are stored in the long-term memory as attractors of autoassociative neural networks. When provoked, networks produce output patterns, which are stored in implicit working memory. These patterns are evaluated and selected. Patterns that are good fit to the given cognitive problem can increase their chance to appear in future generations in two possible, non-exclusive ways: 1) selected patterns are used to train some of the networks (learning) and 2) selected patterns are used as inputs for the networks (provoking). The double dynamics of learning and provoking ensures that superior solutions will dominate the system. Erroneous copying of patterns back to the networks for provoking and learning and noisy recall are the sources of variation (like mutations).

Figure 2.. Schematics of attractor networks searching for the global optimum.

A) Four time steps of selection, from top to bottom. At each step, we only show the network that produces the best output (numbered); the rest of the networks are not depicted. In each time step the networks are provoked by a new pattern that was selected from the previous generation of patterns. Different attractor networks partition the pattern-space differently: blobs inside networks represent basins of attraction. At start, the topmost network (#3) is provoked with an input pattern. It then returns the center of the attractor basin which is triggered by the input. When the output of this network is forwarded as input to the next network (#11), there is a chance that the new attractor basin has a center that is closer to the global optimum. If there is a continuity of overlapping attractor basins through the networks from the initial pattern (top) to the global optimum (bottom), then the system can find the global optimum even without learning. B) Learning in attractor networks. Network #5, when provoked, returns an output pattern that is used to train network #9 (blue arrow). As the network learns the new pattern, the palimpsest memory discards an earlier attractor (with the gray basin), a new basin (purple shape) forms around the new prototype (purple ×) and possibly many other basins are modified (basins with dotted outlines). Black dots indicate attractor prototypes ( i.e. learnt patterns). With learning, successful patterns could spread in the population of networks. Furthermore, if the transmission of patterns between networks is noisy a network might learn a slightly different version of the pattern, new variation is introduced to the system above and beyond the standing variation. This allows the system to find the global optimum even if it was not used to pre-train any network. The gray arrow in the background indicates the timeline of network #9.

Figure 3.. The effect of retraining on the speed of evolution.

Lines represent the evolution in four different populations, where a different number of networks were retrained. Each population consisted of 10 networks (see the rest of the parameters under the Methods section). Thin lines: stochastic attractor dynamics; thick lines: simulated attractor dynamics (abstract networks always return the stored attractor prototype that is closest to the actual input, with 0.001 per bit probability noise; capacity to store C _fix = 30 patterns, μ _O = 0.002). Parameters: N = 200, N _A = 20, μ _T = 0.01, μ _I = 0.005, elitist selection, keeping the best one only from each output generation; random networks are selected for retraining (never the same in a given generation). Fitness is the relative Hamming similarity to the global optimum.

Figure 4.. Fitness and recall accuracy over periodically alternating environments.

Blue: average fitness; green: best fitness; purple: distance of the best output of the population from the closest one stored in memory (for details, see main text). Grey and white backgrounds represent the changing environment: We alternated two global optimums at every 2000 ^th generation. After the 12000 ^th generation, we turned off learning (thick vertical line) and set the input to random patterns after each changing of the environment. Parameters: N _A = 100, N = 100, N _T = 40, fitness is the relative Hamming similarity to the actual optimum.

Figure 5.. Convergence of the actual best fitness of the metapopulation with increasing problem size N on general building block function landscape.

Each curve is an average of 10 independent iterations. N _D = 10 × 10 demes, N _A = 10 networks per deme, N neurons per network, patterns of length N are partitioned to blocks of size P = 10 ( B = N/ P blocks per pattern), p _rec = 0.1, µ _R = 1/N, p _migr = 0.004, N _T = 5. Note the logarithmic x axis. Inset: single simulation at N = 80, B = 8 (other parameters are the same). Plateaus roughly correspond to more and more blocks being optimized by finding the best subsequence on the building-block fitness landscape.