The Role of Vertical Disparity in Distance and Depth Perception as Revealed by Different Stereo-Camera Configurations

Abstract

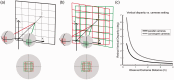
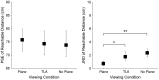
Vertical binocular disparity is a source of distance information allowing the portrayal of the layout and 3D metrics of the visual space. The role of vertical disparity in the perception of depth, size, curvature, or slant of surfaces was revealed in several previous studies using cue conflict paradigms. In this study, we varied the configuration of stereo-cameras to investigate how changes in the horizontal and vertical disparity fields, conflicting with the vergence cue, affect perceived distance and depth. In four experiments, observers judged the distance of a cylinder displayed in front of a large fronto-parallel surface. Experiment 1 revealed that the presence of a background surface decreases the uncertainty in judgments of distance, suggesting that observers use the relative horizontal disparity between the target and the background as a cue to distance. Two other experiments showed that manipulating the pattern of vertical disparity affected both distance and depth perception. When vertical disparity specified a nearer distance than vergence (convergent cameras), perceived distance and depth were underestimated as compared with the condition where vertical disparity was congruent with vergence cues (parallel cameras). When vertical disparity specified a further distance than vergence, namely an infinite distance, distance and depth were overestimated. The removal of the vertical distortion lessened the effect on perceived distance. Overall, the results suggest that the vertical disparity introduced by the specific camera configuration is mainly responsible for the effect. These findings outline the role of vertical disparity in distance and depth perception and support the use of parallel cameras for designing stereograms.

Keywords: cameras configuration; cue conflict; depth perception; distance perception; stereoscopic displays; vertical disparity.

Figure 1.

(a) Retinal projection of a fronto-parallel plane shown on both eyes (top) and the resulting horizontal or vertical disparity shown when both retinas are superimposed (bottom). (b) Retinal projection of stereograms of a fronto-parallel plane captured with convergent cameras, shown on both eyes (top), and the resulting horizontal or vertical disparity shown when both retinas are superimposed (bottom). (c) Retinal vertical disparity of a point with an eccentricity of 30°, and an elevation of 30 degrees, computed for an observer with an inter-ocular distance of 64 mm, converging symmetrically at a 1-m viewing distance. The black line is for an off-axis camera configuration, located and focusing at a 1-m distance. The dotted line represents the vertical disparity for a setting with cameras converging at 1 m, located and focusing at a 1 -m distance.

Figure 2.

Geometrical predictions of the perceived curvature for a fronto-parallel grid (maximum of 30° eccentricity) that consider only the transforms on the pattern of horizontal disparity, for an observer with an inter-ocular distance of 64 mm sitting at 1 m. (a) Predicted percept, a convex plane (the blue grid), for displayed images taken from cameras converging on the middle of a fronto-parallel grid (in dark). (b) A concave plane, the prediction for the condition where the surface is rotated in opposite directions (divergent cameras). In both figures, LE and RE indicate the positions of the left and right eyes, whose visual axes are shown in red and green, respectively.

Figure 3.

An example of a stimulus used in the study, arranged for cross fusion. The background surface and the cylinder are texture-mapped with random-dots. The task could not be performed monocularly. Dots were painted in white over a grey background to minimize crosstalk.

Figure 4.

Perceived reachable distance for the three viewing conditions: stimulus in presence of a background surface (“Plane”), without the surface but with luminance adjustment (“TLA”), or presented alone without adjustment (“No Plane”). Left panel: mean points of subjective equality ; right panel: mean just-noticeable differences. Vertical error bars show 95% bootstrap confidence intervals computed using the bias-corrected and accelerated method (4,000 repetitions), Efron and Tibshirani (1994). Significant differences from post-hoc tests are indicated by * (p < .05) and ** (p < .01).

Figure 5.

The design of stimuli in Experiment 2. Left: Cameras are set convergent leading to distortions in the horizontal and vertical patterns of disparity. Each camera frustum is symmetric. The cameras axis is directed toward the center of interest. The distortions occurred because the rendering plane and the viewing plane have different orientations. Middle: Cameras are set parallel. In the off-axis method, an asymmetric frustum is defined and allows that the rendering plane and the viewing plane match and have the same orientation. No distortions are present; the fronto-parallel plane remains the same. Right: Cameras are also set parallel. However, the images are now rotated, keeping their center aligned with each together, so as they are perpendicular to the line of sight of each eye (divergent cameras).

Figure 6.

Top: Sample psychometric functions for one representative observer. Horizontal error bars show bootstrap confidence intervals of points of subjective equality (estimated using bootstrap resampling). Bottom: Perceived reachable distance for the three camera conditions: “Convergent,” “Parallel,” and “Divergent.” Left panel: mean points of subjective equality; right panel: mean just-noticeable differences. Vertical error bars show 95% bootstrap confidence intervals computed using the bias-corrected and accelerated method (4,000 repetitions), Efron and Tibshirani (1994). Significant differences from post-hoc tests are marked with a ** (p < .01).

Figure 7.

Perceived reachable distance for the three viewing conditions: convex-distortion, “Flat” or no-distortion, and concave-distortion, where vertical parallax was removed. Left panel: mean points of subjective equality; right panel: mean just-noticeable differences. Vertical error bars show 95% bootstrap confidence intervals computed using the bias-corrected and accelerated method (4,000 repetitions), Efron and Tibshirani (1994). Significant differences from post-hoc tests are marked with * (p < .05), ** (p < .01).

Figure 8.

Depth ratios providing the perception of a perfectly circular cylinder for the three experimental conditions: “convergent,” “parallel,” and “divergent.” Depth ratios above 1 correspond to underestimation of depth, and depth ratios below 1 show depth overestimation. Left panel: mean points of subjective equality. The dotted line represents the predicted depth ratios based on the perceived distance measured in Experiment 2. The solid line is the regression line performed on the measured depth ratios. Right panel: mean just-noticeable differences. Vertical error bars show 95% bootstrap confidence intervals computed using the bias-corrected and accelerated method (4,000 repetitions), Efron and Tibshirani (1994). Significant differences from post-hoc tests are marked with *** (p < .001).

Figure 9.

Scatter plots of depth ratios versus distance ratios (left) and of scaling distance versus reachable distance (right) for the three conditions of camera configuration (convergent, parallel, and divergent). Each dot corresponds to individual data. The dotted lines show the linear fits.